Aloha :)
Mit Hilfe des Gauß'schen Integralsatzes \((dV\cdot\vec\nabla=d\vec\sigma)\) führen wir das Integral über die geschlossene Oberfläche \(\partial M\) von \(M\) auf ein Integral über das gesamte Volumen von \(M\) zurück:$$I=\oiint\limits_{\partial M}\vec F\,d\vec\sigma=\oiint\limits_{\partial M}d\vec\sigma\;\vec F=\iiint\limits_MdV\cdot\vec\nabla\vec F=\iiint\limits_M\operatorname{div}\vec F\,dV$$
Die Divergenz des Vektorfeldes ist schnell bestimmt:$$\operatorname{div}\vec F=\operatorname{div}\begin{pmatrix}xz+\frac{x^3}{3}\\[1ex]2ze^{xy}\\[1ex]zy^2-\frac{z^2}{2}-xz^2e^{xy}\end{pmatrix}=\left(z+x^2\right)+2xze^{xy}+\left(y^2-z-2xze^{xy}\right)=x^2+y^2$$
Hier drängt sich die Verwendung von Zylinderkoordinaten geradezu auf:$$\vec r=\begin{pmatrix}r\cos\varphi\\r\sin\varphi\\z\end{pmatrix}\quad;\quad dV=dx\,dy\,dz=r\,dr\,d\varphi\,dz$$weil dann \(\operatorname{div}\vec F=r^2\) wird, was zu einem einfachen Integranden führt:$$\pink{I=\iiint\limits_M r^3\,dr\,d\varphi\,dz}$$Die 3-te Potenz bei \(r^3\) kommt daher, weil das Volumenelement \(dV\) in Zylinderkoordinaten auch noch einen Faktor \(\vec r\) beiträgt.
Damit ist der einfach Teil erledigt. Zur konkreten Berechnung des Integrals brauchen wir noch geeignete Integrationsgrenzen. Dazu müssen wir alle Punkte der Menge \(M\) durch einen Ortsvektor \(\vec r\) in Zylinderkoordinaten beschreiben.$$M=\{(x;y;z\in\mathbb R^3\,\big|\,x^2+y^2\le4\;\land\;0\le z\le1-x\}$$Die Bedinung \(x^2+y^2\le4\) ist schnell in \(\green{r\le2}\) überführt.
Auch die Bedinung \(0\le z\le1-x\) bereitet keine Schwierigkeiten: \(\green{0\le z\le1-r\cos\varphi}\)
Erst die "versteckte" Bedingung \(0\le1-x\) bzw. \(\green{x\le1}\) macht die Sache fummelig. Sie sorgt nämlich dafür, dass der Teil des Zylinders mit \(x>1\) fehlt.
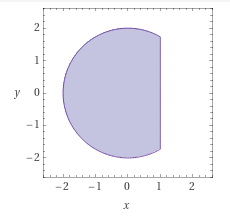
Übertragen auf Zylinderkoordinaten heißt das$$0\le1-r\cos\varphi\implies r\cos\varphi\le1$$Solange \(\green{r\le1}\) ist, können wir \(\varphi\) eine volle Umdrehung laufen lassen:$$\green{\varphi\in[0;2\pi]}\quad\text{für }r\le1$$Sobald aber \(r>1\) wird, können wir mit dem Winkel \(\varphi\) nicht mehr vollständig umlaufen ohne an die rechte Kante zu stoßen:$$r\cos\varphi\le1\implies\cos\varphi\le\frac1r\implies\green{\varphi\in\left[\arccos\frac1r\;;\;2\pi-\arccos\frac1r\right]}\quad\text{für }1<r\le2$$
Zusammengefasst teilen wir daher das Volumen von \(M\) in zwei Volumina auf, die wir durch folgende Parametrisierungen abtasten:$$\vec r_1=\begin{pmatrix}r\cos\varphi\\r\sin\varphi\\z\end{pmatrix}\quad;\quad r\in[0;1]\;;\;\varphi\in[0;2\pi]\;;\;z\in[0;1-r\cos\varphi]$$$$\vec r_2=\begin{pmatrix}r\cos\varphi\\r\sin\varphi\\z\end{pmatrix}\quad;\quad r\in[1;2]\;;\;\varphi\in\left[\arccos\frac1r;2\pi-\arccos\frac1r\right]\;;\;z\in[0;1-r\cos\varphi]$$
Dadurch zerfällt unser pinkes Integral von oben in zwei Teile:$$I=\int\limits_{r=0}^1\;\int\limits_{\varphi=0}^{2\pi}\int\limits_{z=0}^{1-r\cos\varphi}r^3\,dr\,d\varphi\,dz+\int\limits_{r=1}^2\;\int\limits_{\varphi=\arccos\frac1r}^{2\pi-\arccos\frac1r}\int\limits_{z=0}^{1-r\cos\varphi}r^3\,dr\,d\varphi\,dz$$
Die Integration über \(dz\) liefert:$$I=\int\limits_{r=0}^1\;\int\limits_{\varphi=0}^{2\pi}\left(r^3-r^4\cos\varphi\right)dr\,d\varphi+\int\limits_{r=1}^2\;\int\limits_{\varphi=\arccos\frac1r}^{2\pi-\arccos\frac1r}\left(r^3-r^4\cos\varphi\right)dr\,d\varphi$$
Bei der Integration über \(d\varphi\) müssen wir etwas rechnen:$$I=\int\limits_{r=0}^1\left[r^3\varphi-r^4\sin\varphi\right]_{\varphi=0}^{2\pi}\,dr+\int\limits_{r=1}^2\left[r^3\varphi-r^4\sin\varphi\right]_{\varphi=\arccos\frac1r}^{2\pi-\arccos\frac1r}\,dr$$$$\phantom I=2\pi\int\limits_{r=0}^1r^3\,dr+2\pi\int\limits_{r=1}^2r^3\,dr-\int\limits_{r=1}^2r^4\left(\sin\left(2\pi-\arccos\frac1r\right)-\sin\left(\arccos\frac1r\right)\right)dr$$Wegen \(\sin(2\pi-x)=-\sin(x)\) vereinfacht sich das zu:$$$$$$\phantom I=2\pi\int\limits_{r=0}^2r^3\,dr+\int\limits_{r=1}^22r^4\sin\left(\arccos\frac1r\right)dr$$$$\phantom I=2\pi\left[\frac{r^4}{4}\right]_{r=0}^2+\int\limits_{r=1}^22r^4\sqrt{1-\cos^2\left(\arccos\frac1r\right)^2}dr=8\pi+\int\limits_{r=1}^22r^4\sqrt{1-\frac{1}{r^2}}\,dr$$$$\phantom{I}=8\pi+\int\limits_{r=1}^22r^3\sqrt{r^2-1}\,dr=8\pi+\frac{28\sqrt3}{5}$$Das letzte Integral habe ich mir von Wolfram ausrechnen lassen, weil ich jetzt zum Tanzen muss. Das solltest du aber mittels partieller Integration alleine hinkriegen.