Aufgabe:
Ich hab eine 3x3 Matrix
A = ( {0 2 3}
{2 4 -1}
{-4 -2 10} )
gegeben. Dazu soll ich eine LR- Zerlegung berechnen. Die obere Dreiecksmatrix R und die Permutationsmatrix P hab ich schon berechnet.
Problem/Ansatz:
Wie berechne ich nun die untere Dreiecksmatrix?
Vielen Dank im Voraus!
Mein Rechenweg:
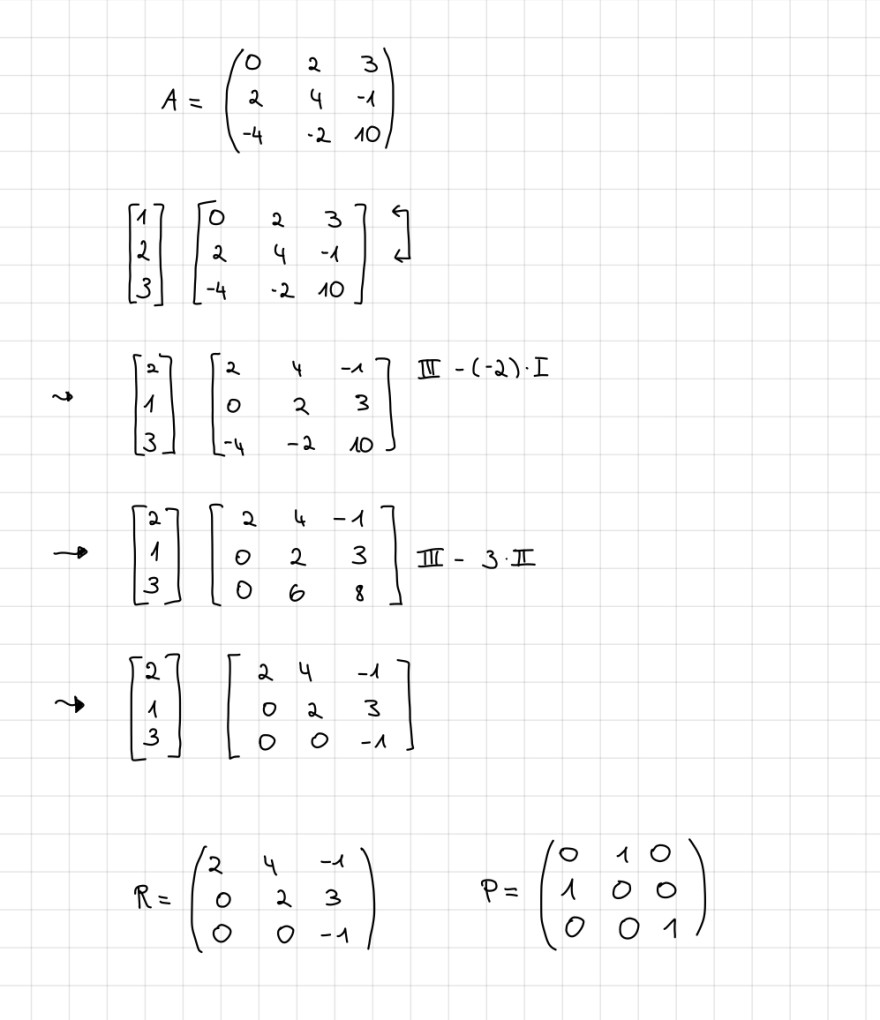
Text erkannt:
\( A=\left(\begin{array}{ccc}0 & 2 & 3 \\ 2 & 4 & -1 \\ -4 & -2 & 10\end{array}\right) \)
\( \left[\begin{array}{l}1 \\ 2 \\ 3\end{array}\right]\left[\begin{array}{ccc}0 & 2 & 3 \\ 2 & 4 & -1 \\ -4 & -2 & 10\end{array}\right] \leftarrow \)
\( \rightarrow\left[\begin{array}{l}2 \\ 1 \\ 3\end{array}\right]\left[\begin{array}{ccc}2 & 4 & -1 \\ 0 & 2 & 3 \\ -4 & -2 & 10\end{array}\right] \mathbb{I I}-(-2) \cdot I \)
\( \rightarrow\left[\begin{array}{l}2 \\ 1 \\ 3\end{array}\right]\left[\begin{array}{rrr}2 & 4 & -1 \\ 0 & 2 & 3 \\ 0 & 6 & 8\end{array}\right] \) III-3·II
\( \rightarrow\left[\begin{array}{l}2 \\ 1 \\ 3\end{array}\right]\left[\begin{array}{ccc}2 & 4 & -1 \\ 0 & 2 & 3 \\ 0 & 0 & -1\end{array}\right] \)
\( R=\left(\begin{array}{ccc}2 & 4 & -1 \\ 0 & 2 & 3 \\ 0 & 0 & -1\end{array}\right) \quad P=\left(\begin{array}{lll}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{array}\right) \)