Berechne den Grenzwert, ohne L`Hopital.

Question

Aufgabe: Berechne den Grenzwert, ohne L`Hopital.

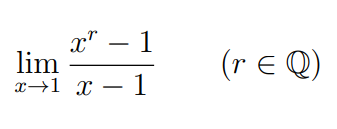
Text erkannt:

\( \lim \limits_{x \rightarrow 1} \frac{x^{r}-1}{x-1} \quad(r \in \mathbb{Q}) \)

Problem/Ansatz:

Komme leider nicht weiter. Habe den Bruch mit der Binomischen Formel erweitert, allerdings hilft es mir nicht wirklich weiter, da die Hochzahl r ist. Wie kann ich den Grenzwert berechnen, ohne dass der Nenner 0 wird ? Darf leider kein L´Hopital verwenden, habe es jedoch getan, um zu sehen was das Ergebnis ist. Habe r als Grenzwert bekommen, weiss aber nicht wie der Lösungsweg dorthin ist.

Mir ist klar, dass es eine ähnliche Frage gibt, jedoch ist die Antwort nicht sehr hilfreich.

Lösungsansätze wären super.

Vielen Dank im Voraus!

Answer 1

Du kannst den Bruch in zwei Faktoren aufsplitten. Außerdem betrachte zunächst nur \(r>0\). Den Fall \(r<0\) handelst du dann per Substitution \(x=\frac 1y\) ab.

Schreibe also \(r = \frac pq\) mit \(p,q\in \mathbb N\).

$$\frac{x^{\frac pq}-1}{x-1} = \frac{x^{\frac pq}-1}{x^{\frac 1q}-1}\cdot \frac{x^{\frac 1q}-1}{x-1}=\ldots$$

Setze nun \(t=x^{\frac 1q}\):

$$\ldots =\frac{t^p-1}{t-1}\cdot \frac{t-1}{t^q-1} =\ldots$$

3. Binomische Formel:

$$\ldots =\sum_{i=0}^{p-1}t^i\cdot \frac{1}{\sum_{i=0}^{q-1}t^i} \stackrel{t\to 1}{\longrightarrow}  \frac pq$$

Comments

Wie kommt man auf so etwas?

Welche Kenntnisse werden vorausgesetzt?

---

@ggT22
Haufenweise die 3. binomische Formel anwenden und haufenweise ineinandergeschachtelte Limites berechnen. :-D