F(x)=0,1x³ für das intervall | = [4, 8]

Question

Gesucht wird der wert der Obersumme O4 und U4 (4 Rechtecke) für die Funktion

F(x)=0,1x³ für das intervall | = [4, 8]

Text erkannt:

- \( f(x)=0,1 x^{3} \) far dos intervall \( 1=[4,8] \)
\begin{tabular}{c|c|c|c|c|c|}
\hline & 10 & \\
\hline & \( x \) & 2 & 4 & 8 & 8 \\
\hline\( y \) & 0,80 & 6,40 & 21,6 & 51,20
\end{tabular}
6.-
2-
\( \frac{1}{2} \)
\( \begin{array}{ll}1 & 6 \\ 4 & 6\end{array} \)
\( x \)

Problem/Ansatz:

Muss ich die 4  ebenfalls durch 4 nehmen? Oder zeigt die 4 einfach nur an wie hoch die y Achse sein soll ohne das ich diese dann durch teilen muss

Comments

Oder ist das so richtig? (Bezüglich der x achse)

Text erkannt:

- \( f(x)=0,1 x^{3} \) for das intervall \( 1=[4,8] \)
\begin{tabular}{c|c|c|c|c|c|c|c|c|}
\( x \) & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
\hline\( y \) & 0,10 & 0,80 & 2,70 & 6,40 & \( 12,592160031,30 \) & 1,20
\end{tabular}

Answer 1

Hallo,

wenn du die Summen in dem Intervall von 4 bis 8 angeben sollst, musst du auch die Wertetabelle entsprechend anpassen. x = 2 interssiert dann gar nicht.

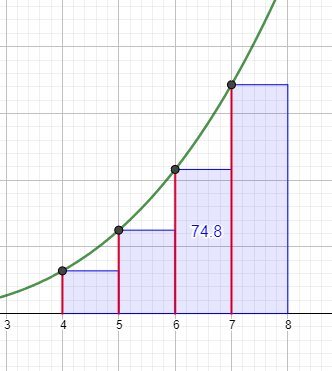
Das Integral von 4 bis 8 beträgt 4 Längeneinheiten. Diese Zahl teilst du durch die Anzahl der Rechtecke, also 4 : 4 = 1.

Die Untersumme besteht also aus vier Rechtecken, deren Breite = 1 ist und deren Höhe dem kleineren Funktionswert der vier Teilintervallen entspricht.

\(U_4=\frac{4}{4}\cdot(f(4)+f(5)+f(6)+f(7))=74,8\)

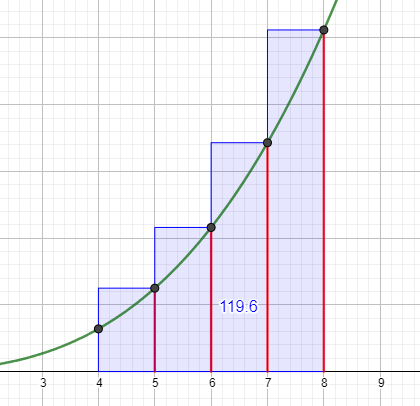
Die Obersumme besteht dann aus vier Rechtecken, deren Breite = 1 ist und deren Höhe dem größeren Funktionswert der einzelnen Teilintervalle entspricht.

\(O_4=\frac{4}{4}\cdot(f(5)+f(6)+f(7)+f(8))=119,6\)

Gruß, Silvia

Comments

Achsooooo danke!!!