Ich denke, wir werden diesen Fläche durch Integration berechnen, aber ich möchte nur wissen, ob wir diesen Fläche zwischen (1 und 3), (-2 und 3) berechnen und alles summieren oder zwischen (1 und 3)
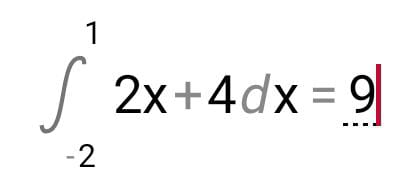
Text erkannt:
\( \int \limits_{-2}^{1} 2 x+4 d x=9 \)
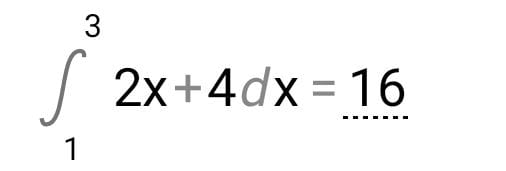
Text erkannt:
\( \int \limits_{1}^{3} 2 x+4 d x=16 \)
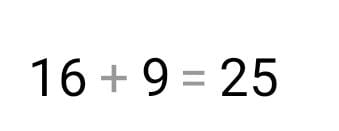
Text erkannt:
\( 16+9=25 \)