integralrechnung sooo schwer

Question

wie lautet die funktion dritten grades f(x)= ax + bx + cxx +d, deren hochpunkt an der stelle -1 liegt, und die den Wendepunkt (1/6) hat und die x-achse bei x=3 schneidet?

Diskutiere die Funktion und gib die wendetangente an
berechne die flächer, die von der kurve und x.achse eingeschlossen wird.


zum haare rupfen!!!!! >-<

Answer 1

rechne erstmal die funktion aus. integrieren kannst du hinterher immer noch.

Answer 2

Hi,

ich liefere mal ein paar Ideen.

 

Bedingungen aus dem Text:

f'(-1) = 0

f(1)=6

f''(1)=0

f(3)=0

sich ergebendes Gleichungssystem:

3a - 2b + c = 0

a + b + c + d = 6

6a + 2b = 0

27a + 9b + 3c + d = 0

Was ergibt:

f(x) = 0,375x^3-1,125x^2-3,375x+10,125

Für die Wendetangente bilde die erste Ableitung und bestimme f'(1).

f'(1) = -4,5

Das entspricht der Steigung der Wendetangenten y = mx+b

m = -4,5...b errechnet sich, wenn wir den Wendepunkt einsetzen:

6 = -4,5 + b

b = 10,5

 

Wendetangente:

y = -4,5x + 10,5

 

Sieht dann so aus:

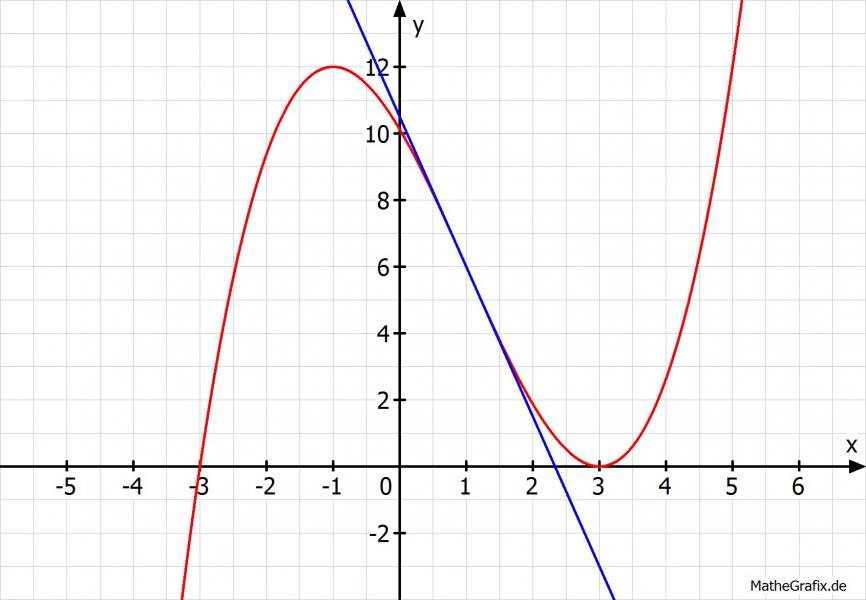
Das Integrieren überlasse ich nun Dir.

Tipps: Wo liegt der Schnittpunkt der rechten und linken Seite (Integralsgrenzen).

Welche Fläche ist überhaupt gesucht und wie berechnet man sie letztlich.

 

Grüße