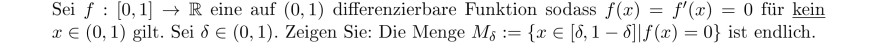
Text erkannt:
Sei \( f:[0,1] \rightarrow \mathbb{R} \) eine auf \( (0,1) \) differenzierbare Funktion sodass \( f(x)=f^{\prime}(x)=0 \) für kein \( x \in(0,1) \) gilt. Sei \( \delta \in(0,1) \). Zeigen Sie: Die Menge \( M_{\delta}:=\{x \in[\delta, 1-\delta] \mid f(x)=0\} \) ist endlich.
Aufgabe:
Problem/Ansatz:
Ich habe leider keine Idee dazu. Kann mir vielleicht jemand dabei weiterhelfen?…