Funktion auf lokale Extremstellen untersuchen / Gleichung umformen für kritische Stellen

Question

Aufgabe:

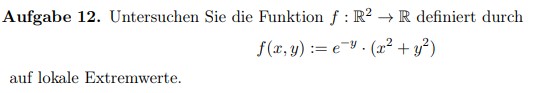
Text erkannt:

Aufgabe 12. Untersuchen Sie die Funktion \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) definiert durch
\( f(x, y):=e^{-y} \cdot\left(x^{2}+y^{2}\right) \)
auf lokale Extremwerte.

Problem/Ansatz:

Grundsätzlich weiß ich wie ich vorgehen muss. Ich habe folgende Ableitungen:

dx: 2xe^-y und

dy: 2e^-y y - e^-y *x² - e^-y *y²

Diese setze ich gleich null. Wenn ich bei dx umforme nach x erhalte ich: -e^-y /2. Bei der anderen Gleichung weiß ich gar nicht wie ich vorgehen soll. Kann ich das Ergebnis aus der ersten Gleichung irgendwie sinnvoll nutzen? Wie soll ich weiter vorgehen um auf die kritischen Stellen zu kommen? Danach weiß ich wahrscheinlich auch wieder alleine weiter.

Danke

Answer 1

Die einzige Lösung der Gleichung 2xe^-y=0 ist x=0.Damit vereinfacht sich

2e^-y y - e^-y *x² - e^-y *y²=0

zu

2e^-y y - e^-y *y²=0

Klammere hier noch e^-y aus und löse 2y-y²=0.

Comments

Alles klar, danke sehr!