Aufgabe:
a) Es sei X eine exponentialverteilte Zufallsvariable mit Dichtefunktion
\( f(x)=\left\{\begin{array}{ll}2 e^{-2 x} & , x \geq 0 \\ 0 & , x<0\end{array}\right. \)
Der Erwartungswert E(X) der Zufallsvariable X ist dann gegeben durch das uneigentliche Integral
\( E(X)=\int \limits_{0}^{\infty} x \cdot f(x) d x \)
Berechnen sie diesen Erwartungswert mittels partieller Integration.
b) Bestimmen sie zur Funktion
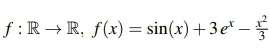
die Stammfunktion F mit F(0)=1.
Problem: Hat jemand evtl. hierzu ausführliche Rechen- und Lösungswege? Ich bedanke mich im voraus, mfg