Erwartungswert aus stückweise konstanter Dichtefunktion (Grafik)

Question

Aufgabe:

Die Zufallsvariable X hat eine stückweise konstante Dichtefunktion f.

Diese ist nachfolgend gegeben durch ihren Graphen. Berechnen Sie den Erwartungswert E(X).

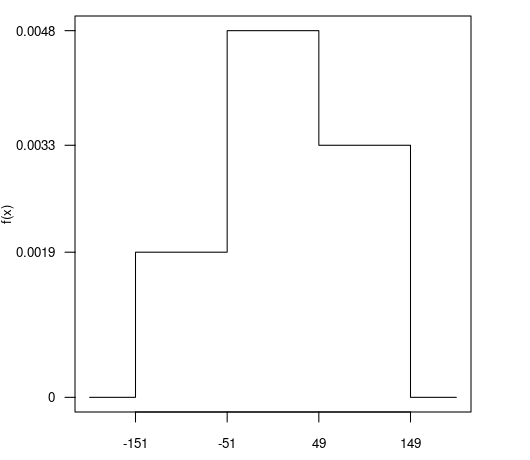
Problem/Ansatz:

Ich bin gerade leicht verwirrt, ob ich die Fläche unter der "Kurve" oder das Integral bestimmen muss. Wenn ich Stumpf die Fläche berechne (100*0,0019+100*0,0048+100*0,0033=1 ist das Ergebnis falsch.

Über das Integral komme ich auf:

-19,19 + 0,48 + 32,67 = 13,96

stimmt das?

Ich weiß, die Frage wurde schon öfters gestellt, ich bin mir aber unsicher, weil hier durch den mittleren Bereich (-51 bis 49) sich das Vorzeichen ändert und ich so über das Integral einen sehr kleinen Wert (0,48) im Vergleich zu den anderen herauskommt. Das kann ich gerade nicht nachvollziehen, weil die Geometrische Fläche ja ähnlich groß wie die anderen sein sollte. Oder sollte ich das Integral teilen (von -51 bis 0 und von 0 bis 49), sodass sich die Fläche dort nicht aufhebt?

Answer 1

Die Formel 100*0,0019+100*0,0048+100*0,0033=1 entspricht dem Integral der Dichtefunktion, und das muss 1 ergeben. Eben daraus folgt, dass in jedem Balken 100 Werte liegen.

Der Erwartungswert errechnet sich deshalb wie folgt:

E = \( 0.0019 \sum\limits_{k=0}^{99}{(-151+k)} +  0.0048 * \sum\limits_{k=0}^{99}{(-51+k)}  + 0.0033 * \sum\limits_{k=0}^{99}{(49+k)} \)

E = \( -19.285 - 0.72 + 32.505 = 12.5 \)

Auf das gewünschte Ergebnis von 13 kommt man, wenn man nicht von ganzen Zahlen ausgeht, sondern von den Mittelwerten dazwischen:

E = \( 0.0019 \sum\limits_{k=0}^{99}{(-150.5+k)} +  0.0048 * \sum\limits_{k=0}^{99}{(-50.5+k)}  + 0.0033 * \sum\limits_{k=0}^{99}{(49.5+k)} = 13 \)

Comments

das kann ich nachvollziehen, allerdings sollte das korrekte Ergebnis 13,0 sein. Das verstehe ich nicht...

---

Siehe die Ergänzung in meiner Antwort.