Wie viel m² Kletterfläche stehen ungefähr zur Verfügung?

Question

Aufgabe:

m² kletterfläche

Problem/Ansatz:

,,Der Kegel" in Berlin ist der höchste Kletterturm der Bundeshauptstadt. Der Turm hat einen Umfang von 44m. Der untere zylindrische Teil ist 10,70 m und der obere Kegel 8 m hoch.

Wie viel m² Kletterfläche stehen ungefähr zur Verfügung?

Answer 1

Hallo,

Die Mantelfläche eines Zylinders berechnest du mit \(M=U\cdot h\). Beides ist gegeben.

Die Mantelfläche eines Kegels berechnest du mit \(M=\pi\cdot \red r\cdot \blue s\)

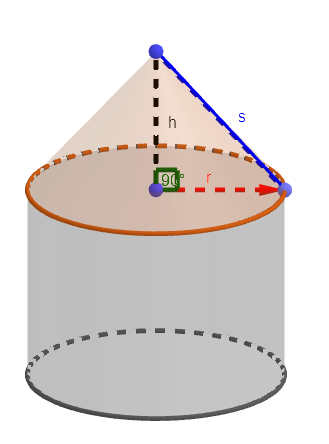
r erhältst du, indem du aus der Umfangsgleichung des Zylinders \(44=2\cdot r\cdot \pi\)
s ist die Hypotenuse des rechtwinkligen Dreiecks, die du mit dem Satz des Pythagoras berechnen kannt.

Melde dich, falls du noch Fragen hast.

Gruß, Silvia

Answer 2

Hallo

aus dem Umfang und der Höhe des Zylinders  die Mangelfächer ausrechnen, dann den Radius des Kreises des Kegels aus dem Umfang berechnen mit Pythagoras die Seitenlänge aus Radius und Höhe und damit den Mantel des Zylinders . Formeln dazu aus der Formelsammlung oder eurem Unterricht

Gruß lul

Answer 3

U = 2·pi·r = 44 --> r = 7.003 m

A1 = U·h1 = 44·10.7 = 470.8 m²

A2 = U/2·√(r^2 + h2^2) = 44/2·√(7.003^2 + 8^2) = 233.9 m²

A = 470.8 + 233.9 = 704.7 m²