Aus Eigenschaften einer ganzrationalen Funktion eine Funktionsgleichung

Question

Aufgabe:

Hallo, meine Schwester ist in der Oberstufe und war eine lange Zeit krank. Sie hat diese Aufgabe als einzige bekommen. Sie sollte aus den Eigenschaften einer Funktion die Funktionsgleichung rechnerisch rausfinden. Im Anhang ist die Aufgabe mit ihrer Lösung. Es wäre nett, wenn jemand darüber schauen könnte, ob diese richtig ist . Vielen Dank im voraus .

Answer 1

Hallo,

Wendestelle ist xW=1. (Wegen der Symmetrie auch bei x=-1.)

W(-1|0) ist aber falsch, da y nicht gleich Null sein muss.

Die zweite Ableitung ist falsch. Hinter der 2 fehlt das c.

f''(x)=12ax^2+2c

Also

f(2)=0=16a+4c+e

f'(2)=2=32a+4c → 1=16a+2c

f''(1)=0=12a+2c

16	4	1	0
32	4	0	2
12	2	0	0

2. Zeile durch 2

16	4	1	0
16	2	0	1
12	2	0	0

2. Zeile minus 3. Zeile → 2. Zeile

16	4	1	0
4	0	0	1
12	2	0	0

3. Zeile minus 3* 2. Zeile

16	4	1	0
4	0	0	1
0	2	0	-3

Zeilen sortieren und noch etwas bearbeiten

1	0	0	0,25
0	1	0	-1,5
0	0	1	2

a=0,25; c=-1,5; e=2

\(f(x)=0,25x^4-1,5x^2+2\)

https://www.desmos.com/calculator/poiq2tfb5i

:-)

Comments

Hallo,

Vielen Dank für die Antwort. Das heißt das xW= -1  ist . Die zweite Eigenschaft ist also xW=-1. Wäre das

Text erkannt:

Aufgale
Der Graph einer ganzrationalen Funktion 4.Grades ist
symmetrisch zur y-Achse. Im Punkt \( \mathrm{P}(2 / 0) \) hat der Graph
die Steigung 2. und bei \( x W=1 \) befindet sich eine
Wendestelle.
4. Grades: \( \quad \begin{aligned} & f(x)=a x^{4}+b x^{3}+c x^{2}+d x+e \\ & f(x)=a x\end{aligned} \)
5 Eigenochaften: nur gerade Eponeuten
I. \( P\left(\frac{x}{2}(0)\right. \)
II \( f^{\prime}(1)=2 \)
\( 2 x^{1} \)
\( \begin{aligned} f^{\prime}(2) & =2 \\ \text { t } 0 & =a \cdot 2^{4}+c \cdot 2^{2}+e \\ \text { II } 2 & =4 \cdot a \cdot(2)^{7}+2 \cdot c \cdot 2 \\ \text { III } 0 & =12 \cdot a \cdot(-1)^{2}+2 c \end{aligned} \)
\( \left|\begin{array}{ccc} 16 a+4 c+1 e & 0 \\ 32 a+4 c+0 & 2 \\ -12 & 0 & 0 \end{array}\right|\left|\begin{array}{cccc} 16 & 4 & 1 & 0 \\ 32 & 4 & 0 & 2 \\ 48 & 2 & 0 & 0 \end{array}\right| \rightarrow b= \)

Wäre das so ungefähr richtig.

Grüße :)

---

Die zweite Eigenschaft ist also xW=-1.

Diese Eigenschaft enthält keine neue Information, da sie sich aus der Achsensymmetrie ergibt.

Außerdem muss es in der untersten Zeile

12  2  0  0

heißen.

---

Ja das habe ich danke. Ist die Antwort o,5 x^4 -2 denn richtig ?

---

Leider immer noch nicht richtig.

Ich habe meine Antwort ergänzt.

Answer 2

Hallo,

ein Fehler ist hier

Die Wendestelle ist bei x = 1 und nicht bei x = 2, außerdem fehlt das "c" nach der 2.
Daher lautet die 3. Gleichung \(0=12a+2c\)


Gruß, Silvia

Comments

Hallo,

Vielen Dank für die Antwort. Ja das war ein Schusselfehler von mir. Ist der Wendepunkt aber nicht -1. Ebenso, wollte ich fragen, wie sie auf diese Funktionsgleichung/Graphen gekommen sind.

Tut mir leid, ich habe mich verschrieben, der Wendepunkt ist bei -1

Ich hatte das noch mal so gemacht.

Text erkannt:

Aufgale
Der Graph einer ganzrationalen Funktion 4.Grades ist
symmetrisch zur y-Achse. Im Punkt \( \mathrm{P}(2 / 0) \) hat der Graph
die Steigung 2. und bei \( x W=1 \) befindet sich eine
Wendestelle.
4. Grades: \( \quad \begin{aligned} & f(x)=a x^{4}+b x^{3}+c x^{2}+d x+e \\ & f(x)=a x\end{aligned} \)
5 Eigenochaften: nur gerade Eponeuten
I. \( P\left(\frac{x}{2}(0)\right. \)
II \( f^{\prime}(1)=2 \)
\( 2 x^{1} \)
\( \begin{aligned} f^{\prime}(2) & =2 \\ \text { t } 0 & =a \cdot 2^{4}+c \cdot 2^{2}+e \\ \text { II } 2 & =4 \cdot a \cdot(2)^{7}+2 \cdot c \cdot 2 \\ \text { III } 0 & =12 \cdot a \cdot(-1)^{2}+2 c \end{aligned} \)
\( \left|\begin{array}{ccc} 16 a+4 c+1 e & 0 \\ 32 a+4 c+0 & 2 \\ -12 & 0 & 0 \end{array}\right|\left|\begin{array}{cccc} 16 & 4 & 1 & 0 \\ 32 & 4 & 0 & 2 \\ 48 & 2 & 0 & 0 \end{array}\right| \rightarrow b= \)

Wäre das genauso richtig, oder können Sie mir helfen, was hier falsch sein könnte. Gruß J

---

Tut mir leid, ich habe mich bei der Aufgabenstellung verschrieben der Wendepunkt ist bei -1

---

Ob die Wendestelle bei x = 1 oder x = -1 ist, spielt hier keine Rolle, denn die 2. Ableitung lautet \(f''8x)=12ax^2+2c\).

 \((-1)^2=1^2=1\)

Wie du auch aus dem gezeichneten Graphen erkennen kannst. Wegen der Symmetrie zur y-Achse gibt es einen Wendepunkt bei x = 1 und x = -1.

Die dritte Zeile lautet somit 12 2 0 0 und nicht -12 2 0 0

---

Hallo,

Vielen Dank. Ja ich hatte ein Denkfehler. Vielen vielen Dank. Ich habe es nochmal gerechnet und hab dies raus.

Text erkannt:

übemepangsale: steckoriefaufgale ser solurienig
Aufgate
Der Graph einer ganzrationalen Funktion 4.Grades ist
symmetrisch zur y-Achse. Im Punkt \( \mathrm{P}(2 / 0) \) hat der Graph
die Steigung 2. und bei \( \mathrm{xW}=1 \) befindet sich eine
Wendestelle.
4. grade:: \( \begin{aligned} f(x) & =a x^{4} \\ f(x) & =b x^{6}+c x^{2}+d x^{1}+e\end{aligned} \)
5 Eigenochaften : ner gerade eppreutan
I. \( P\left(\frac{x}{2}(0)\right. \)
II \( f^{\prime}(1)=2 \)
\( f(x)=a x^{4}+c x^{2}+e \quad 3 \) Eigemerafsen I.
I. \( p(210) \)
\( x_{1} \cdot f^{\prime}(2)=2 \)
\( (0)=110) \Rightarrow f^{\prime \prime}(-1)=0 \)
\( =1 \quad \rho^{\prime \prime}(-1)=0 \)\( \quad \begin{array}{l}f^{\prime}(x)=4 a x^{3}+2 c x^{1} \\ f^{\prime \prime}(x)=12 a x^{2}+2 c\end{array} \)
\( \begin{array}{l} \text { I. } 0=a \cdot 2^{4}+c \cdot 2^{2}+e \\ \text { II } 2=4 \cdot a \cdot(2)^{7}+2 \cdot c \cdot 2 \\ \text { III } 0=12 \cdot a \cdot(-1)^{2}+2 c \\ 0=12 a+2 c \hat{p}_{\text {potivi }}+2 \end{array} \)
\( \begin{array}{l} f(x)=-0,25 x^{4}-1,5 x^{2}+2 \\ \end{array} \)

---

So weit, so gut. Dein Ergebnis für a ist

und in der Gleichung schreibst du

---

Schon wieder ein. Fehler habe ich gemacht….. so ist es natürlich richtig?

Text erkannt:

\( \begin{array}{l}f(x)=0,25 x^{4}-1,5 x^{2}+2 \\\end{array} \)

---

Jetzt stimmt es!

Answer 3

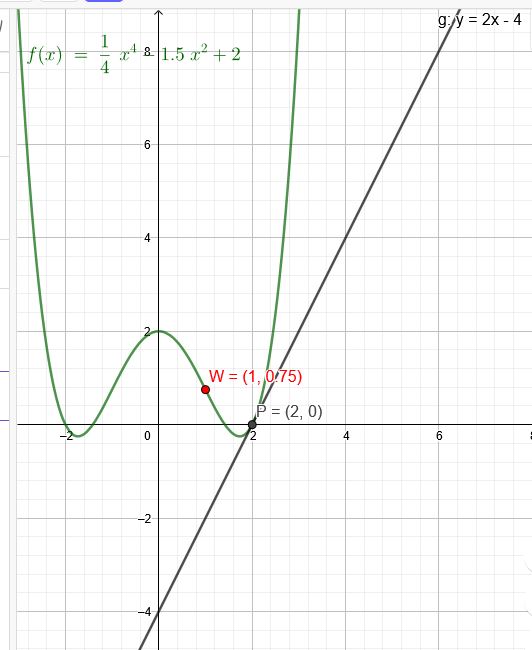
\(f(x)=a*x^4+c*x^2+e\)

\(P(2|0)\)

\(f(2)=a*2^4+c*2^2+e=16a+4c+e=0\)

1.)\(16a+4c+e=0\)

Steigung ist \(2\) in \(P(2|0)\)

\(f´(x)=4a*x^3+2c*x\)

\(f´(2)=4a*2^3+2c*2=32a+4c=2\)

2.)\(32a+4c=2\) → \(16a+2c=1\)

Bei \(x_W=1\) ist eine Wendestelle

\(f´´(x)=12a*x^2+2c\)

\(f´´(1)=12a+2c=0\)

3.)\(12a+2c=0\)→\(2c=-12a\)    in 2.)   \(16a-12a=1\)→\(a= \frac{1}{4} \)

\(c=-6a\)→ \(c=-6*\frac{1}{4} =-1,5\)

1.)\(16*\frac{1}{4}+4*(-1,5)+e=0\) →  \(4-6+e=0\) →  \(e=2\)

\(f(x)=\frac{1}{4}x^4-1,5*x^2+2\)

Comments

Vielen vielen Dank. Ich habe mich aber bei der Aufgabenstellung  verschrieben der Wendepunkt ist bei -1.

---

Vielen vielen Dank. Ich habe mich aber bei der Aufgabenstellung verschrieben der Wendepunkt ist bei -1.

Da \(f(x)\) symmetrisch zur y-Achse ist, ist sowohl bei \(x=1\) als auch bei

\(x=-1\) eine Wendestelle.