Erwartungswert ausrechnen, Unbekannte

Question

Aufgabe:

Gegeben sci eine Zufallsvariable \( X \) mit folgender Wahrscheinlichkeitsmassenfunktion:

\( f(x)=\left\{\begin{array}{cc} 0.25 & , x=1 \\ 0.1 & , x=2 \\ 3 a-0.45 & , x=3 \\ b & , x=4 \\ 0 & , \text { sonst } \end{array}\right. \)

Weiterhin sei bekannt, dass \( b=a+0.1 \) ist.

Problem/Ansatz:

Irgendwie komme ich nicht auf das richtige Ergebnis..Wollte den Erwartungswert ausreichnen: Kriege für a = 0,125 raus, ist das richtig? Wenn ich es einsetze kriege ich ein anderes Ergebnis als in der Musterlösung raus

Comments

Ich erhalte eon anderes Ergebnis als Du.

Wie hast Du gerechnet?

---

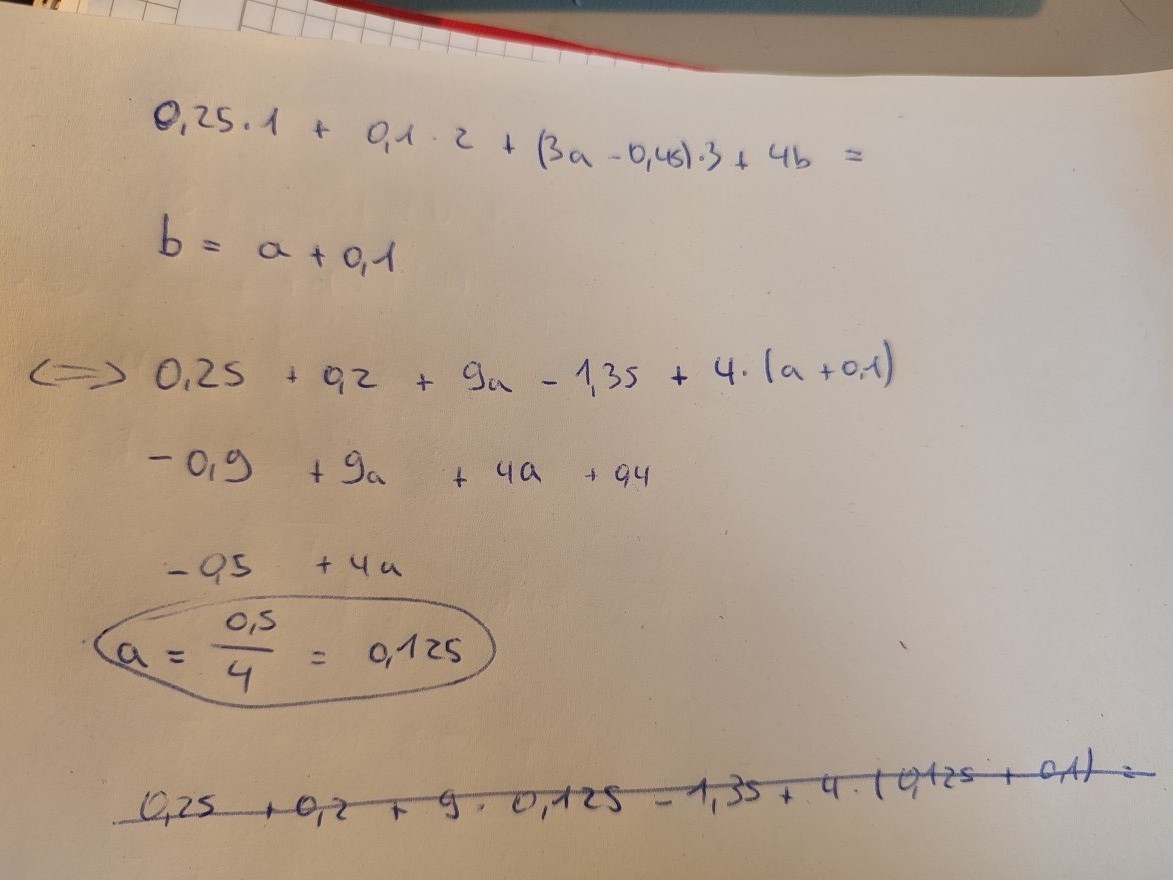
Text erkannt:

\( \begin{aligned} & 0,25 \cdot 1+0,1 \cdot 2+(3 a-0,45) \cdot 3+4 b= \\ & b=a+0,1 \\ \Leftrightarrow & 0,25+0,2+9 a-1,35+4 \cdot(a+0,1) \\ - & 0,9+9 a+4 a+94 \\ - & =0,5+4 a \\ a= & \frac{0,5}{4}=0,125\end{aligned} \)
\( 0,25+0,2+9 \cdot 0,125-1,35+4 \cdot(0,125+0,1)= \)

@mathehilf

Sry, Bild ist blöd ausgerichtet

---

also wenn du den Erwartungswert ausrechnen willst, brauchst du erstmal den Wert von a. Aus deiner Aufschrift erkenne ich überhaupt nicht, welche Gleichung du aufgestellt hast, denn theoretisch bestimmst du a erstmal damit, dass du weißt, die Punktwahrscheinlichkeiten müssen aufaddiert 1 ergeben. Das wäre für a=0,25 der Fall. Was steht in deiner Musterlösung für ein Wert für a? Ansonsten rechne dann den Erwartungswert für a=0,25 aus.

---

Achso, jetzt verstehe ich es. Aber sollte man nicht mit auflösen nach a die 0,25 rausbekommen? Es gibt keine Lösung für a aber für den Erwartungswert: 2,75

---

Das ist doch ein Widerspruch in sich! Wenn a=0,35 ist, dann gibt es doch (eben diese) Lösung für a!

Dass ist 3a-0,45=0,3.

b ist dann 0,25+0,1=0,35.

Probe:

0,25+0,1+0,3+0,35=1.

Answer 1

Löse das Gleichungssystem

        \(\begin{aligned}0.25 + 0.1 + (3\cdot a-0.45) + b &= 1\\b&=a+0.1\end{aligned}\)

um \(a\) und \(b\) zu berechnen.

Answer 2

Löse das Gleichungssystem

0.25 + 0.1 + (3·a - 0.45) + b = 1
b = a + 0.1

Ich erhalte: a = 0.25 ∧ b = 0.35

Berechne jetzt den Erwartungswert

E(X) = 1·0.25 + 2·0.1 + 3·(3·0.25 - 0.45) + 4·0.35 = 2.75

Comments

Wieso das =1 ?

---

Die Summe aller Wahrscheinlichkeiten bei einer Wahrscheinlichkeitsmassenfunktion beträgt 1 = 100%. Irgendetwas davon muss ja eintreten.