Flächenberechnung bei b) und c) der Aufgabe?

Question

Aufgabe:

Am Ufer der Ostsee wird ein 500 Meter langer Deich gebaut, der das abgebildete Profil erhalten soll. Er kann durch eine Parabel und zwei geraden modelliert werden. Die Parabel läuft horizontal aus.

Problem/Ansatz:

Ich habe a) schon, jedoch weiß ich nicht wie man b) und c) berechnet.

Also wie man bei b) die Fläche unter der Parabel durch Integral, dazu Rechteck und Dreieck berechnet.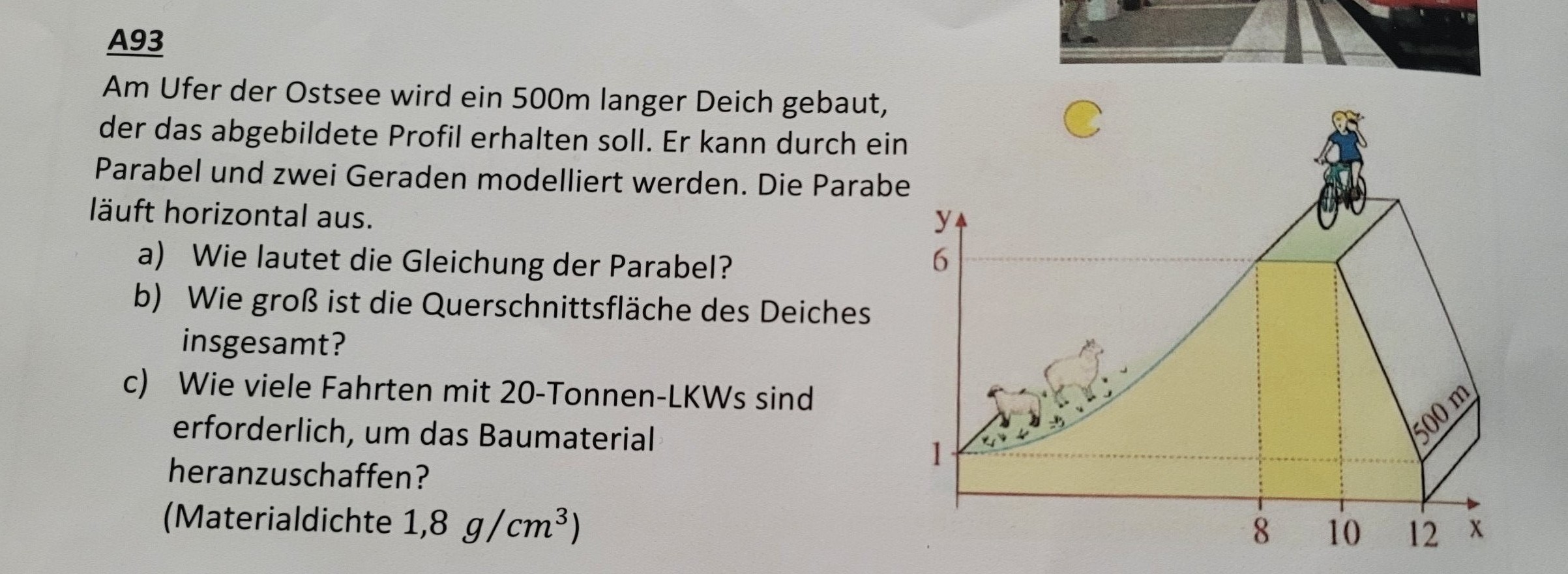

Text erkannt:

A93
Am Ufer der Ostsee wird ein \( 500 \mathrm{~m} \) langer Deich gebaut, der das abgebildete Profil erhalten soll. Er kann durch ein Parabel und zwei Geraden modelliert werden. Die Parabe läuft horizontal aus.
a) Wie lautet die Gleichung der Parabel?
b) Wie groß ist die Querschnittsfläche des Deiches insgesamt?
c) Wie viele Fahrten mit 20-Tonnen-LKWs sind erforderlich, um das Baumaterial heranzuschaffen?
(Materialdichte \( 1,8 \mathrm{~g} / \mathrm{cm}^{3} \) )

Comments

Flächenberechnung bei b) und c) der Aufgabe?

Bei c) geht es nicht um eine Flächenberechnung.

Answer 1

Die Fläche unter der Parabel erfordert zunächst die Parabelgleichung mit dem Ansatz f(x)=ax²+1. Einsetzen des Punktes (8|6) ergibt eine Bestimmung von a. Die Querschnittsfläche der Deiches ist dann \( \int\limits_{0}^{8} \)f(x) dx + Trapezfläche.

Comments

Also die Gleichung hatte ich aus a) schon. Kannst du damach bitte genauer erklären

---

Integral: gelbe Fläche. Trapez: graue Fläche

Answer 2

a) Wie lautet die Gleichung der Parabel?

Scheitel \(S(0|1)  \)

\(f(x)=a*x^2+1\)

\(P(8|6)  \)

\(f(8)=a*8^2+1=64a+1=6\)    → \(64a=5\)     →  \(a=\frac{5}{64}\)

\(f(x)=\frac{5}{64}*x^2+1\)

Comments

Das hatte ich schon kannst du mir bei b und c helfen. Ich hatte es in die Beschreibung geschrieben.

---

Du hast drei Teilflächen: grüne Fläche unterhalb der Parabel bis x = 8, dann blaues Rechteck und zuletzt das rote Trapez.

---

Also mit meiner Gleichung erst im Intervall 0 bis 8, dann 8 bis 10 und dann 10 bis 12 rechnen. Um am Ende einfach diese drei Lösungen mal 3 rechnen und bin ich dann fertig?

---

Oder nur von 8 bis 10?

---

1. Das Intervall von 0 bis 8

2. Das Rechteck mit 6 x 2 m = ....   (Die blaue 6 in meiner Skizze ist falsch)

3. Das Trapez mit \( A=\frac{a+c}{2} \cdot h \)

a = 1, g = 6 und h = 2

---

Bei 3) von dir, was ist c und warum gibt es g obwohl du es nicht in die Gleichung geschrieben hast.

---

Ich habe mich verschrieben, also c = 6. Beim Trapez berechnest du die Fläche mit der Summe aus Grundseite und der darüber liegenden parallelen Seite mal der Höhe, egal wie sie heißen.

---

Danke ich komme auf 40,3 Flächeneinheiten und was muss ich bei c) machen.

---

Multipliziere dein Ergebnis mit 500, damit du das Gesamtvolumen des Deiches hast.

Wandle das Ergebnis in Kubikzentimeter um, multipliziere es mit 1,8 und du hast das Gewicht des Baumaterials in g. Wandle es in t um und dann... ?

---

Naja ich verstehe es nicht, aber trotzdem danke bis hier hin. Ich frage mal jemand anderen.

---

Was verstehst du nicht? Um das Volumen zu berechnen, multiplizierst die ausgerechnete Fläche mit 500m Deichlänge. Dann hast du ein Ergebnis in Kubikmeter.

Materialdichte \( 1,8 \mathrm{~g} / \mathrm{cm}^{3} \)

Da die Dichte in 1,8g pro Kubikzentimeter angegeben ist, musst du die Kubikmeter entsprechend umwandeln. Ist das soweit klar?

---

Nein leider ich weiß nicht was ich rechnen muss.

---

40,3 x 500 = 20150 Kubikmeter = 20.150.000.000 Kubikzentimeter

x 1,8 : 1.000.000 = 36.270 t

36.270 : 20 = 1.813,5, also werden 1.814 LKW benötigt.

Rechne sicherheitshalber nochmal nach!

Answer 3

a)

Parabel mit dem Scheitel S(0 | 1) durch den Punkt P(8, 6)

a = (Py - Sy)/(Px - Sx)^2 = 5/8^2 = 5/64

f(x) = 5/64·x^2 + 1

b)

A1 = ∫ (0 bis 8) (5/64·x^2 + 1) dx = 64/3

A2 = 6·2 = 12

A3 = 1/2·(6 + 1)·2 = 7

A = 64/3 + 12 + 7 = 121/3 = 40.33 m²

c)

p = 1.8 g/cm³ = 1.8 kg/dm³ = 1.8 t/m³

m = 121/3·500·1.8 = 36300 t

Wenn ein 20t-LKW 20t Zuladung hat dann:

36300 / 20 = 1815 Fahrten