Question

Wie kommt man beim Erweitern und Ausmultiplizieren auf die folgende Lösung?

Ich habe mich bereits an der Aufgabe versucht, komme aber nicht auf das Endergebnis, welches am Ende der Aufgabe steht.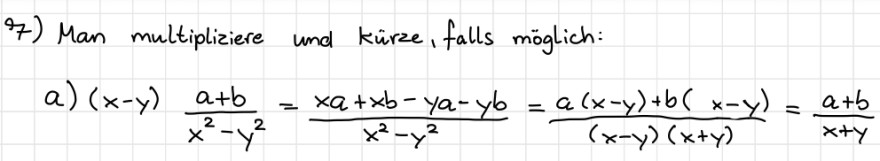

Text erkannt:

7) Man multipliziere und kürze, falls möglich:
a) \( (x-y) \frac{a+b}{x^{2}-y^{2}}=\frac{x a+x b-y a-y b}{x^{2}-y^{2}}=\frac{a(x-y)+b(x-y)}{(x-y)(x+y)}=\frac{a+b}{x+y} \)

Answer 1

Du kannst sofort kürzen: (x-y)/((x+y)(x-y)) = 1/(x+y)

Das Ganze mal (a+b) -> (a+b)/(x+y)

Ausmultiplitieren ist unnötig,

Comments

Ausmultiplitieren ist unnötig,

Da hast du vollkommen Recht. Dass der Original-
Aufgabensteller dies anrät (oder gar verlangt)
ist pseudo-didaktischer Mist.

Answer 2

\( (x-y) \frac{a+b}{x^{2}-y^{2}}=\frac{x a+x b-y a-y b}{x^{2}-y^{2}}=\frac{a(x-y)+b(x-y)}{(x-y)(x+y)}=\frac{a+b}{x+y} \)

Ich schreibe es mal auf, ohne den Zähler auszumultiplizieren :

\( \frac{(x-y)*(a+b)}{x^2-y^2}=\frac{(x-y)*(a+b)}{(x-y)*(x+y)}=\frac{a+b}{x+y} \)