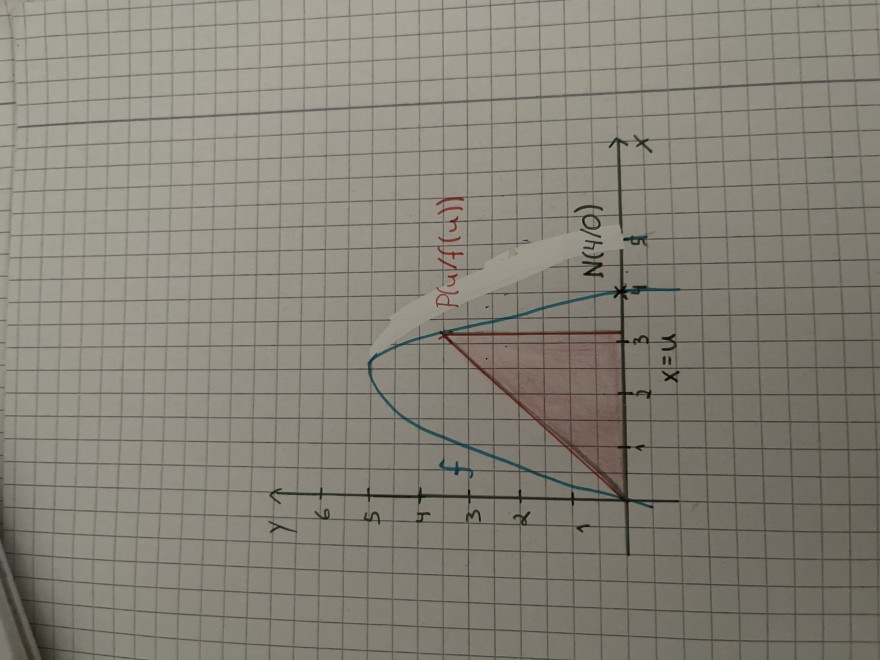
Aufgabe:
Der Punkt P (u/f(u)) wandert auf dem Graphen der Funktion f mit f(x)=1/5x • (x-4)•(x-8) zwischen den Punkten O(0/0) und N(4/0).
Der Flächeninhalt A des eingefärbten Dreiecks hängt von der Lage P ab. Zeichnen Sie den Graphen der Zielfunktion A und ermitteln den Wert von u, bei den der Flächeninhalt des Dreiecks maximal ist.
Geben Sie diesen Flächeninhalt an.
Problem/Ansatz:
Hallo,
Ich verstehe nicht, was ich mit den angegeben Schnittpunkt N von f mit der x-Achse anfangen kann. Wie komme ich denn auf die Informationen die ich brauche um den maximal möglichen Flächeninhalt auszurechnen? Ich habe die Funktion aufgelöst und dann die Ableitung gemacht aber da kriege ich falsche Werte raus