Integral für E[X^2] bekomme ich nicht geknackt

Question

Aufgabe: Gegeben ist die Dichtefunktion. Bestimme den Erwartungswert ( E[X^2] ) wie folgt:

\( \int \limits_{-\infty}^{\infty}-x^{2} \cdot 2 \cdot \frac{x}{a} e^{\frac{x^{2}}{a}} d x \) 

Problem/Ansatz:

Ich bekomme das Integral nicht geknackt, obwohl ich es mit partieller Integration und Substitution versucht habe.

Mache ich es zu kompliziert?

Comments

Ich bekomme das Integral nicht geknackt

Wenn du damit meinst, keine Stfkt gefunden zu haben : Das ist nicht schlimm

---

Was ist denn da die Dichte?

Answer 1

Aloha :)

Der Integrand$$f(x)=-\frac{2x^3}{a}e^{\frac{x^2}{a}}$$ist eine punktsymmetrische Funktion:$$f(-x)=-\frac{2(-x)^3}{a}e^{\frac{(-x)^2}{a}}=\frac{2x^3}{a}e^{\frac{x^2}{a}}=-f(x)$$Daher heben sich alle Beiträge links von der \(y\)-Achse gegen alle Beiträge rechts von der \(y\)-Achse gegenseitig auf.

Das heißt, das Integral ist \(=0\).

~plot~ 2x^3/12*e^(x^2/12) ; [[-3|3|-5|5]] ~plot~

Comments

Zur vollständigen Begründung fehlt der Nachweis der Existenz des Integrals.

---

$$\lim\limits_{c\to\infty}\int\limits_{-c}^cf(x)\,dx=\lim\limits_{c\to\infty}0=0$$

---

Das entspricht nicht der Definition des uneigentlichen Riemann Integrals und ebenfalls nicht der in der Wahrscheinlichkfitstheotie üblichen Lebesgue-Integrierbarkeit.

---

Übrigens, was ist die Dichte?

---

Das sagt Wolfram Alpha zu dem Integral:

---

Wie schon zuvor erklärt, beziehe ich mich u.a. auf die Definition des uneigentlichen Rieman-Integrals - wie es zum Beispiel in Wikipedia erklärt wird und auch in der Literatur üblich ist.

Daneben gibt es den Begriff des Cauchy-Hauptwerts, der sehr selten benötigt wird.

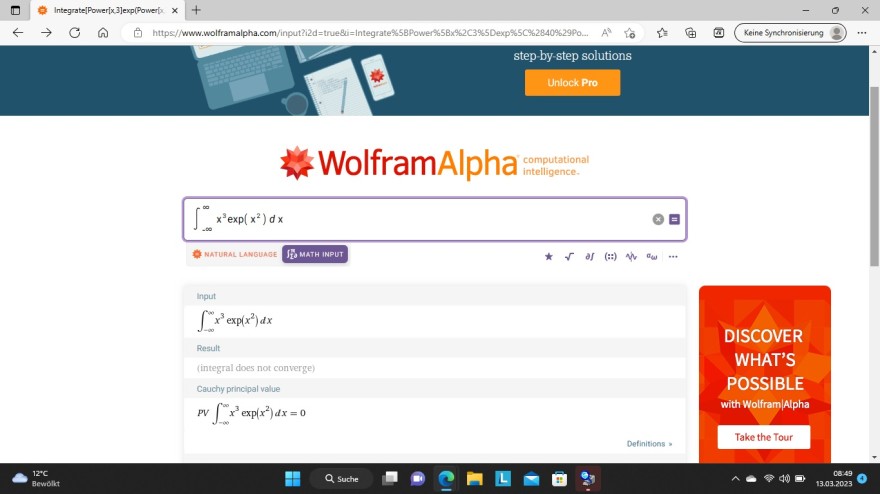
Im übrigen habe ich ein anderes Wolfram-Alpha

Außerdem kann ein Erwartungswert über x^2 als Integrand nur eine nichtnegative Funktion haben.