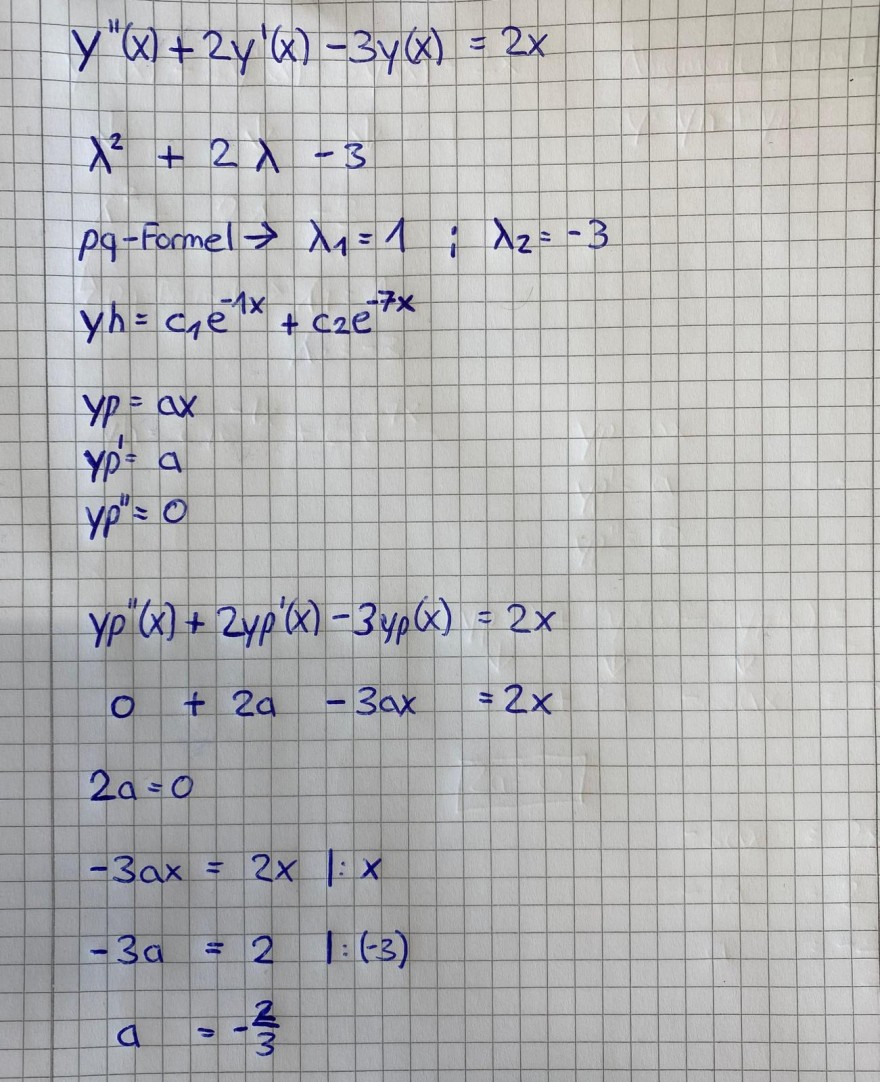
Text erkannt:
\( \begin{array}{l}y^{\prime \prime}(x)+2 y^{\prime}(x)-3 y(x)=2 x \\ \lambda^{2}+2 \lambda-3 \\ p q-\text { Formel } \rightarrow \lambda_{1}=1 ; \lambda_{2}=-3 \\ y h=c_{1} e^{-1 x}+c_{2} e^{-7 x} \\ y p=a x \\ y p^{\prime}=a \\ y p^{\prime \prime}=0 \\ y p^{\prime \prime}(x)+2 y p^{\prime}(x)-3 y p(x)=2 x \\ 0+2 a-3 a x=2 x \\ 2 a=0 \\ -3 a x=2 x \quad / : x \\ -3 a=2 \quad / :(-3) \\ a=-\frac{2}{3}\end{array} \)
Kann mir einer sagen ob ,,2a=0" stimmt? Ich habe die Lösung von einem Kommilitonen aber ich weiß nicht woher der die Annahme hat, dass 2a=0 wäre.
PS: Ist leider alles untereinander, ich weiß nicht wie ich Absätze im Programm mache, tut mir leid.. DANKE für jede antwort!!!