Darstellungsmatrix bzgl. verschiedener Basen bestimmen

Question

Aufgabe:

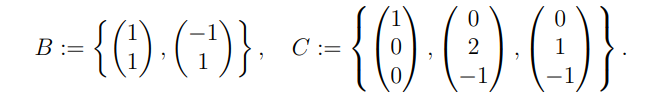
Problem/Ansatz:

Guten Tag, möchte sicher gehen, dass ich die oben genannte Aufgabe richtig gelöst habe.

Meine Idee: Die Basis Vektoren von B in die Abbildung einsetzen und anschließend in die Basis C umwandeln.

Bedeutet:

Für L((1,1)) = (1, 1, -1)

Für L(-1, 1) = (-1, 1, -1)

Also die Darstellungsmatrix bzgl Basis B lautet: ((1,1, -1), (-1, 1, -1))

Anschließend in die Basis C umwandeln das ergibt:

(1,1,-1) = ( 1, 2, -3)

und

(-1, 1, -1) = (-1, 0, 1)

Meine gesuchte Darstellungsmatrix 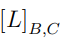lautet also: ((1, 2, -3), (-1, 0, 1))

Würde mich freuen, wenn dies jemand überprüfen könnte oder mich verbessern könnte.

Vielen Dank :)

Comments

Ist die Farstellung für (1,1,-1) on der Basis C nicht eher (1,0 1)?

Ergebnis ist eine 3-2-Matrix , also sind die berechneten Koordinatenvektoren als Spalten zu schreiben.

---

Stimmt habe mich verguckt vielen Dank.

Könntest du mir evtl. verraten woher du weißt, dass das Ergebnis eine 3-2-Matrix ist?

---

Das muss zu L passen, also Bilddimension gleich 3  Argumentdinension gleich 2.

Vergleiche mit der Lösung von T

Answer 1

Aloha :)

$$L_{B,C}=\underbrace{\left(\begin{array}{rrr}1 & 0 & 0\\0 & 2 & 1\\0 & -1 & -1\end{array}\right)^{-1}}_{\text{von E3 nach C}}\cdot\underbrace{\left(\begin{array}{rr}1 & 0\\0 & 1\\0 & -1\end{array}\right)}_{\text{Abb.-Matrix von E2 nach E3}}\cdot\underbrace{\left(\begin{array}{rr}1 & -1\\1 & 1\end{array}\right)}_{\text{von B nach E2}}=\left(\begin{array}{rr}1 & -1\\0 & 0\\1 & 1\end{array}\right)$$