Der Beweis dafür, dass eine mathematische Aussage höheren Grades wahr ist, stützt sich auf Aussagen tieferen Grades, deren Wahrheitsgehalt vorausgesetzt werden darf. Diese Voraussetzung ist erfüllt, wenn die Aussagen des tieferen Grades entweder bewiesen werden konnten oder wenn sie als absolut richtig erkannte Grundsätze eingestuft werden – als gültige Wahrheiten also, die keines Beweises bedürfen. Solche als absolut richtig erkannten Grundsätze nennt die Mathematik Axiome. Die Mathematik macht also ausschließlich Wenn-Dann-Aussagen der Art: Wenn die Axiome (einschließlich derer des Schließens) wahr sind, dann sind auch die daraus geschlossenen Aussagen wahr. Die Aussagen der Mathematik sind – entgegen landläufiger Überzeugung – nicht ausschließlich per se wahr. Außer den Axiomen sind auch die Definitionen wahre Aussagen. Die Aussage ‚Eine Strecke ist die kürzeste Verbindung zweier Punkte‘ definiert den Begriff ‚Strecke‘. Die Aussage ‚Ein Fußball ist eine kugelförmige Lederhülle, die mit eine Luftblase gefüllt ist und einen Umfang von mindestens 68 cm und höchstens 70 cm hat‘ definiert den Begriff Fußball.
In unserer Kommunikation gibt es sehr viele Aussagen, die von keinem Teilnehmer an der Kommunikation bezweifelt werden. Das gilt ganz sicher für fast alle Definitionen alltäglicher Begriffe und auch für einige Sachverhalte in der uns umgebenden Umwelt. Die Aussage ‚Jeden Morgen geht die Sonne auf‘ ist wahr, weil unsere Erfahrung keinen einzigen Fall kennt, der diese Wahrheit widerlegt. Wahrheit gibt es also
- per definitionem
- aus Erfahrung
- durch Übereinkunft.
Auch im Rahmen schulischen Mathematiktreibens muss man auf Aussagen zurückgreifen können, die aus einem dieser drei Gründe wahr sind. Eine Sonderrolle spielt hier die Wahrheit durch Übereinkunft. Die axiomatische Mathematik, wie sie an der Hochschule betrieben wird, hat in der Schule keinen Platz. Übereinkunft wird in der Schule insbesondere dann erzielt, wenn sie sich auf Evidenz gründet, auf Aussagen wie ‚Flächen die sich überschneidungsfrei und vollständig mit paarweise kongruenten Teilflächen überdecken lassen, haben die gleiche Flächengröße.‘ Diese Aussage ist die Grundlage fast aller Beweise des Satzes von Pythagoras. Wer diese Aussage nicht für wahr hält, kann an einer Kommunikation zu einer Reihe von mathematischen Themen nicht teilnehmen.
Die Aussage ‚Der Scheitel eines gestreckten Winkels liegt auf der gleichen Gerade, wie seine beiden Schenkel‘ ist eine Definition des Begriffes ‚gestreckter Winkel‘ und es kann keine Diskussion über den Wahrheitsgehalt von Definitionen geben. Der Aussage ,Ein gestreckter Winkel hat die Größe 180°‘ unterliegt die Übereinkunft, jedem Winkel eine Größe zuzuordnen. Wer diese Übereinkunft nicht akzeptieren will, kann ebenfalls an einer Kommunikation zu einer Reihe von mathematischen Themen nicht teilnehmen. Die Aussage ‚Die Summe der Innenwinkelgrößen eines Dreiecks beträgt 180°‘ muss gegenüber denjenigen SuS begründet werden, denen sie nicht evident erscheint. Die Begründung kann sich dabei nur auf Aussagen stützen, deren Wahrheitsgehalt nicht angezweifelt wird. Und Wahrheit gibt es – wie gesagt – nur
- per definitionem
- aus Erfahrung
- durch Übereinkunft.
Eine häufig anzutreffende Begründung der Aussage ‚Die Summe der Innenwinkelgrößen eines Dreiecks beträgt 180°‘ besteht darin, zwei Innenwinkel des Dreiecks an den dritten so anzulegen, dass alle drei Winkel zusammen einen gestreckten Winkel ergeben. Theoretisch kann man sich einen Schüler vorstellen, der den getreckten Winkel entweder nicht erkennt oder seine Entstehung nicht zwingend findet. Diesem Schüler musste man dann Begründungen liefern, die geeignet sind, seine Zweifel auszuräumen. Sollten dabei Wechselwinkel angeführt werden, müsste genau genommen auch der Wechselwinkelsatz begründet werden. Da auf diese Weise aber theoretisch eine endlose Kette von Begründungen entstehen könnte, wird an einer Stelle abgebrochen und der Schüler kann an einer weiteren Kommunikation zu diesem Thema nicht mehr teilnehmen.
Wie wir also gesehen haben, gibt es in der Auseinandersetzung mit mathematischen Aussagen und ihrem Wahrheitsgehalt immer wieder Situationen, die SuS von einer Kommunikation ausschließen. Ein guter Unterricht vermeidet solche Situationen soweit das überhaupt möglich ist. Vollständig vermeiden kann man solche Situationen aber nicht in jedem Einzelfalle.
Weiter oben hatte ich einen Schüler vorgestellt, der den getreckten Winkel entweder nicht erkennt oder seine Entstehung nicht zwingend findet. Diesem kann vielleicht geholfen werden, indem man ihn auffordert, zwei Ecken des Dreiecks abzureißen und an die dritte anzulegen oder aber man beginnt mit der Winkelsumme im Rechteck und geht dann durch Zerschneiden und neu zusammenlegen des Rechtecks zur Winkelsumme im Parallelogramm über. Dann ist das entlang einer Diagonalen halbierte Parallelogramm ein Dreieck und die Halbierung überträgt sich auf die Winkelsumme. Eine dritte Möglichkeit ist die Vorlage dieses Arbeitsblattes:
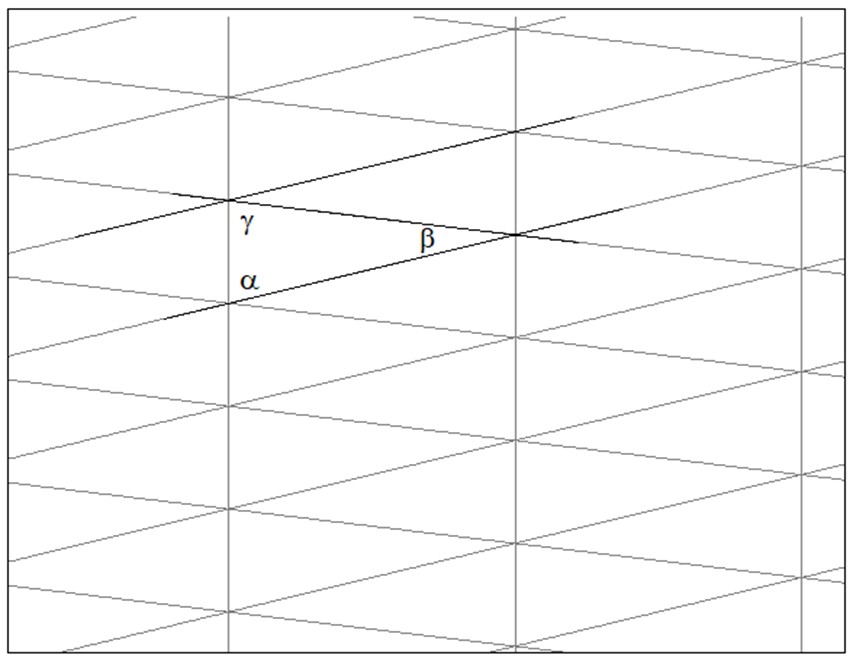
Verbunden mit den Fragen ‚Wo überall kommen die Winkel α, β und γ auf dieser Seite vor?‘ Und ‚Was gilt für α+β+γ?‘
Gleichgültig, welchen Weg man wählt, man wird SuS nur zur Einsicht in den Winkelsummensatz bringen, wenn der Punkt erreicht wird, an dem SuS sagen: Jetzt sehe ich es! Schulunterricht greift letztlich immer auf Evidenzen zurück, von denen nicht vorhersehbar ist, ob das Offensichtliche auch von allen SuS gesehen wird.