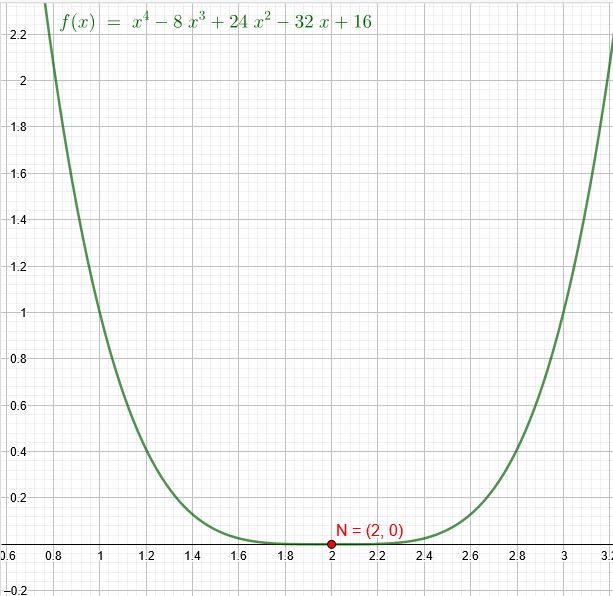
Ich habe Wolfram zur Lösung eingesetzt:
\( y=x^4 -8x^3+24x^2-32x+16 \)
\(y=(x-N_1)*(x-N_2)*(x-N_3)*(x-N_4)\)
\(y=(x-r)*(x-s)*(x-t)*(x-u)\)
\(y=r s t u - r s t x - r s u x - r t u x - s t u x + r s x^2 + r t x^2 + s t x^2 + r u x^2 + s u x^2 + t u x^2 - r x^3 - s x^3 - t x^3 - u x^3 + x^4\)
\(y=r s t u - x*(r s t + r s u + r t u +s t u) + x^2*(r s + r t + s t + r u + s u + t u ) - x^3*(r +s + t +u ) + x^4\)
1.)
\(r s t u=16\)
2.)
\( r s t + r s u + r t u +s t u=32 \)
3.)
\(r s + r t + s t + r u + s u + t u=24\)
4.)
\(r +s + t +u=8\)
\(r=2\) \(s=2\) \(t=2\) \(u=2\)
\(y=(x-2)*(x-2)*(x-2)*(x-2)\)
\(y=(x-2)^4\) hat eine vierfache Nullstelle.