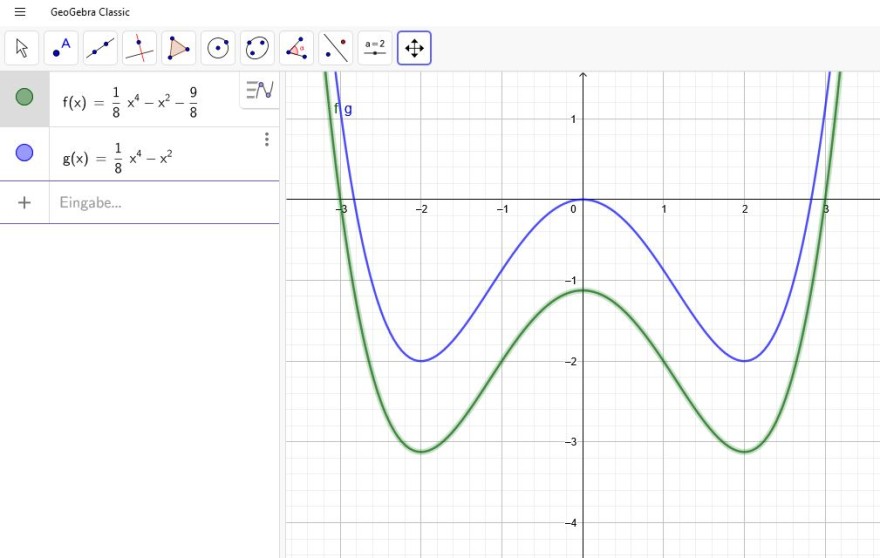
\(f(x)= \frac{1}{8}x^4-x^2-\frac{9}{8}\)
\(f´(x)= \frac{1}{2}x^3-2x\)
\( \frac{1}{2}x^3-2x=0\)
\( x^3-4x=0\)
Satz vom Nullprodukt:
\( x_1=0\) \( x_2=2\) \( x_3=-2\)
\(f(0)= \frac{1}{8}*0^4-0^2-\frac{9}{8}=-\frac{9}{8}\)
\(f´(0)= \frac{1}{2}*0^3-2*0=0\)
Art des Extremwertes:
\(f´´(x)= \frac{3}{2}x^2-2\)
\(f´´(0)= \frac{3}{2}*0^2-2=-2<0 \) →Maximum
Nun kannst du den Graphen von f(x) um \(\frac{9}{8}\) Einheiten nach oben schieben, und du bekommst das Maximum bei E(0|0). Es ist dann auch eine doppelte Nullstelle.
Bei \(f(x)= \frac{1}{8}x^4-x^2-\frac{9}{8}\) hast du 2 Nullstellen in ℝ
Durch das Verschieben des Graphen gibt es somit noch 2 weitere Nullstellen, also insgesamt 4.