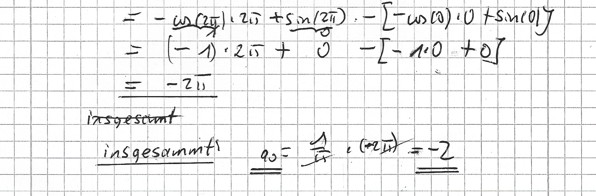Hallo,
a) Ermitteln Sie die Koeffizienten \( a_{0}, a_{1} \) und \( b_{1} \) der Fourier-Reihe \( F_{\mathrm{f}} \) von \( f \).
b) Wie lautet \( F_{\mathrm{f}}\left(\frac{\pi}{2}\right) \) ?
allgemein:
Fourierreihe:
\( f(x)=\frac{a_{0}}{2}+a_{1} \cos (x)+a_{2} \cos (2 x)+a_{3} \cos (3 x)+\ldots+b_{1} \sin (x)+b_{2} \sin (2 x)+b_{3} \sin (3 x)+\ldots \)
= \( \frac{a0}{2} \) + a1 cos(x) +b1 sin(x)
= -1 -1/2 *0 +π sin(\( \frac{π}{2} \))
= -1 +π
oder, in Summenschreibweise,
\( f(x)=\frac{a_{0}}{2}+\sum \limits_{n=1}^{\infty}\left(a_{n} \cos (n x)+b_{n} \sin (n x)\right) \)