Frage: Wie komme ich hier auf z = -1,7507?

Question

Sie erheben in einem Elektrogroßmarkt die Anzahl der verkauften neuen Fernsehgeräte pro Tag. Sei X die Anzahl der verkauften Fernseher pro Tag, dann ergibt sich folgende Verteilung für X:

X	0	1	2	3	4
P(X=x)	0,01	0,06	0,05	0,17	0,71

Sie wollen Ihre Lagerhaltung optimieren. Wie viele Fernseher sollten Sie lagern, wenn die Wahrscheinlichkeit, dass nach 100 Tagen Lagerrückstände bleiben, nur 0.04 betragen soll. Nehmen Sie dazu nur an, dass die Verkäufe einzelner Tage voneinander unabhängig sind und verwenden Sie den Zentralen Grenzwertsatz. (Runden Sie das Ergebnis kaufmännisch auf eine ganze Zahl!) Lösung: 335

Frage: Wie komme ich hier auf z = -1,7507?

Text erkannt:

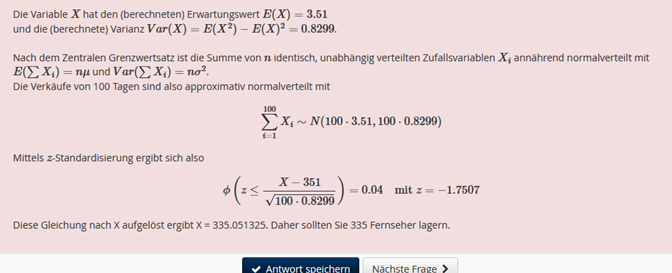
Die Variable $X$ hat den (berechneten) Erwartungswert $E(X)=3.51$
und die (berechnete) Varianz $\operatorname{Var}(X)=E\left(X^{2}\right)-E(X)^{2}=0.8299$
Nach dem Zentralen Grenzwertsatz ist die Summe von $n$ identisch, unabhängig verteilten Zufallsvariablen $X_{i}$ annährend normalverteilt mit $E\left(\sum X_{i}\right)=n \mu$ und $\operatorname{Var}\left(\sum X_{i}\right)=n \sigma^{2}$
Die Verkäufe von 100 Tagen sind also approximativ normalverteilt mit
$\sum \limits_{i=1}^{100} X_{i} \sim N(100 \cdot 3.51,100 \cdot 0.8299)$
Mittels $z$-Standardisierung ergibt sich also
$\phi\left(z \leq \frac{X-351}{\sqrt{100 \cdot 0.8299}}\right)=0.04 \text { mit } z=-1.7507$
Diese Gleichung nach $\mathrm{X}$ aufgelost ergibt $\mathrm{X}=335.051325$. Daher sollten Sie 335 Fernseher lagern.

Comments

Danke, hat sich erledigt. Hab das Quantil übersehen... xD

Answer 1

Wie komme ich hier auf z = -1,7507?

Aus der Normalverteilungastabelle

NORMAL(z) = 0.04 --> z = -1.750686075