Aufgabenstellung:
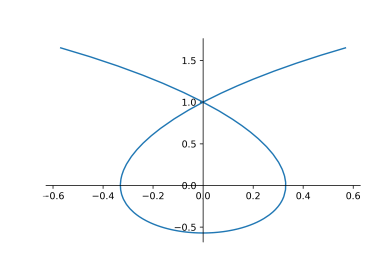
Für die verlängerte Zykloide mit \( x(t)=t-\frac{\pi}{2} \sin (t), y(t)=1-\frac{\pi}{2} \cos (t) \) bestimmen Sie den Flächeninhalt der Schleife, d.h. \( t \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \) (siehe Abbildung).
Lösung:
Es bezeichne \( B \) die gesuchte Fläche der Schleife und es sei das \( C^{1} \)-Vektorfeld \( v \) definiert durch \( v(x, y)=(0, x)^{T} . \) Dann gilt mit der Greenschen Formel
\( \int \limits_{\partial B}\langle v, d x\rangle=\int \limits_{B}\left(\partial_{1} v_{2}-\partial_{2} v_{1}\right) d(x, y)=\int \limits_{B} 1 d(x, y) \)
Also ist das Integral \( \int \limits_{\partial B}\langle v, d x\rangle \) gerade der Flächeninhalt der Schleife. Der Rand von \( B \) hat nach Aufgabenstellung die Parameterdarstellung
\( \gamma(t)=\left(\begin{array}{c} t-\pi / 2 \cdot \sin (t) \\ 1-\pi / 2 \cdot \cos (t) \end{array}\right) \)
für \( t \in[-\pi / 2, \pi / 2] \). Achtung: diese wird so durchlaufen, dass \( B \) stets rechts im Bezug auf die Durchlaufrichtung liegt (im Uhrzeigersinn). Wir kehren für die korrekte Anwendung der Greenschen Formal also die Umlaufrichtung um. Damit gilt dann insgesamt
\( \begin{aligned} \int \limits_{\partial B}\langle v, d x\rangle &=\int \limits_{-\pi / 2}^{\pi / 2}\left\langle(0,-t-\pi / 2 \cdot \sin (-t))^{T},(-1+\pi / 2 \cdot \cos (t), \pi / 2 \cdot \sin (t))^{T}\right\rangle d t \\ &=\int \limits_{-\pi / 2}^{\pi / 2}(-t-\pi / 2 \cdot \sin (-t)) \cdot \pi / 2 \cdot \sin (t) d t=\frac{\pi^{3}}{8}-\pi \approx 0.7342 \end{aligned} \)
Frage:
Wie komme ich hier auf die Funktion v(x,y)?