Nun - Du machst Dir eine Zeichnung und überlegst Dir, wie die X- und Y-Koordinaten von \(\alpha\) aussehen, wenn der Kreis mit dem Radius \(r\) um den Winkel \(\Theta\) abgerollt ist.
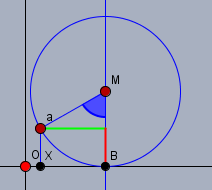
Der blaue Winkel sei \(\Theta\). Dann befindet sich der Berührpunkt \(B\) an der Position \((r\cdot \Theta, 0)\). Die grüne Strecke ist \(=r \cdot \sin \Theta\) daraus folgt dann die X-Koordinate - also die Strecke \(OX\)
$$x(\Theta)= r\cdot \Theta -r \cdot \sin (\Theta)=r( \Theta- \sin (\Theta)) $$
und die Y-Koordinate ist identisch mit der Länge der roten Strecke -und die ist
$$y(\Theta)=r-r\cdot \cos(\Theta)=r(1-\cos(\Theta))$$
Demnach ist \(\alpha(\Theta)\)
$$\alpha(\Theta)=\left(r( \Theta- \sin (\Theta)) , \space r(1-\cos(\Theta)) \right)$$
Gruß Werner