Funktionen, Scheitelformen, Scheitelpunkte und Achsenschnittpunkte bestimmen

Question

die oben Aufgeführten sachen sollen wir berechenen.

Gegeben haben wir P₁ (-3,-4)

                                P₂ (2,-4)

                                P3 (3,-10)

 

Leider weiß ich noch nicht mal wie ich damit anfangen soll weil wir so was noch  nie gerechnet haben.

deswegen währe ich über Hilfe sehr dankbar.

 

Lg

Comments

Hallo Toni, damit du eine Antwort verstehst, ist es sinnvoll, wenn du erst mal die einführenden 3 konstenlosen Videos zu Parabelgleichungen hier anschaust: https://www.matheretter.de/mathe-videos?s=quadratische

---

Ich habe sie mir alle 3 angeschaut!

Danke für den Link

Answer 1

P₁ (-3,-4), P₂ (2,-4), P3 (3,-10)

Da der Funktionswert bei -3 und bei 2 jeweils -4 ist muss sich der Scheitelpunkt zwischen -3 und 2 bei -0.5 befinden. Die Scheitelpunktform lautet daher

f(x) = a·(x + 0.5)^2 + b

Ich setzte hier 2 Punkte ein

f(2) = a·(2 + 0.5)^2 + b = 6.25·a + b = -4

f(3) = a·(3 + 0.5)^2 + b = 12.25·a + b = -10

Wir erhalten 2 Gleichungen und lösen das Gleichungssystem

6.25·a + b = -4
12.25·a + b = -10

II - I

6·a = -6
a = -1

6.25·a + b = -4
b = 2.25

Die Funktionsgleichung lautet also

f(x) = - (x + 0.5)^2 + 2.25 = - x^2 - x + 2

Scheitelpunkt bei S(-0.5 | 2.25)

Y-Achsenabschnitt f(0)

f(0) = - (0 + 0.5)^2 + 2.25 = 2

Nullstellen f(x) = 0

- (x + 0.5)^2 + 2.25 = 0
x = -2 ∨ x = 1

 

Comments

Vielen dank für die Hilfe!

Ich habe später auch noch ein paar Aufgaben zu berechnen bei denen die Punkte nicht den selben y-Wert haben...wie gehe ich an die ran?


Gruß

---

Da stellst du dann über die Normalform ein Gleichungssystem auf

f(x) = ax^2 + bx + c

Ich kann da eventuell noch mal ein Video zu machen. Am besten schreibst du eine neue Aufgabe dazu.

Answer 2

So was nennt man Steckbriefaufgabe.

P₁ (-3,-4) ,     P₂ (2,-4),  P₃ (3,-10)

Du weisst, dass eine Parabel symmetrisch ist bezüglich Spiegelung an der Vertikalen, die durch den Scheitelpunkt geht. Zeichne die 3 Punkte im Koordinatensystem ein (zumindest im Kopf).

Nun siehst du, dass P₁ und P₂ auf der gleichen Höhe liegen. Spiegelungsachse in der Mitte. Scheitelstelle bei x = (-3+2)/2 = -0.5

Ansatz für die Parabelgleichung

y = a(x -(-0.5))^2 + c = a(x+0.5)^2 + c

Nun zwei Punkte einsetzen.

-10 = a(3.5)^2 + c         (I)

-4 = a(2.5)^2 + c           (II) 
------------------------------------- (I) - (II)
-6 = a(3.5^2 - 2.5)^2) = a*6

-6/6 = a = -1

in (I) einsetzen: -10 = -12.25 + c

2.25 = c

y = -(x+0.5)^2 + 2.25 ist die Funktionsgleichung

Scheitelpunkt S(-0.5| 2.25)

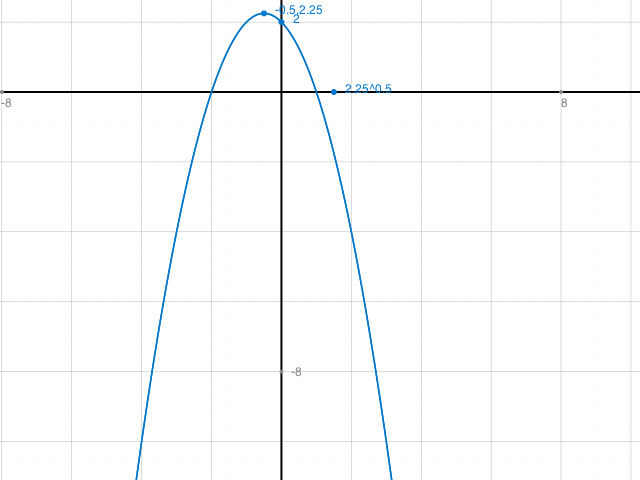
Hier (unten) eine Skizze. Du kannst noch näher ranzoomen mit : https://www.matheretter.de/tools/funktionsplotter/

Beschriftet sind: Scheitelpunkt S(-0.5, 2.25) und y-Achsenabschnitt y=2. Daher y-Achsenschnittpunkt P(0,2).

Der eingezeichnete Punkt auf der x-Achse ist bedeutungslos. Du musst die Schnittpunkte mit der x-Achse noch berechnen. 

 -(x+0.5)² + 2.25 = 0

2.25 = (x+0.5)^2
±1.5 = x+0.5

-0.5 ± 1.5 = x

x₁ = -2, x₂ = 1

Schnittpunkte mit der x-Achse : R(-2|0) und S(1|0).
 

Comments

Dankeschön!

Unser Lehrer sagte uns wir sollen solche Aufgaben mit hilfe von Matrizen lösen...ist das in deinen Augen sinvoll?


Gruß

---

Wenn man geometrische Eigenschaften ausnützen kann, geht das schneller von Hand. Der Taschenrechner macht vielleicht weniger Rechenfehler. Dafür ist das Übertragen der Zahlen vom Blatt auf den Rechner und zurück fehleranfällig.

---

Mit Matrizen meint man hier die linearen Gleichungssysteme in Matrizenform ohne die Variablen.

Eigentlich finde ich es nicht so Sinnvoll.
Unter anderem weil der Schreibaufwand dadurch nicht wesentlich minimiert wird und das Verständnis von Gleichungen verloren geht.

Ich finde es zunächst sinnvoller bei den Gleichungen zu bleiben.

Aber das kannst du auch total anders sehen.