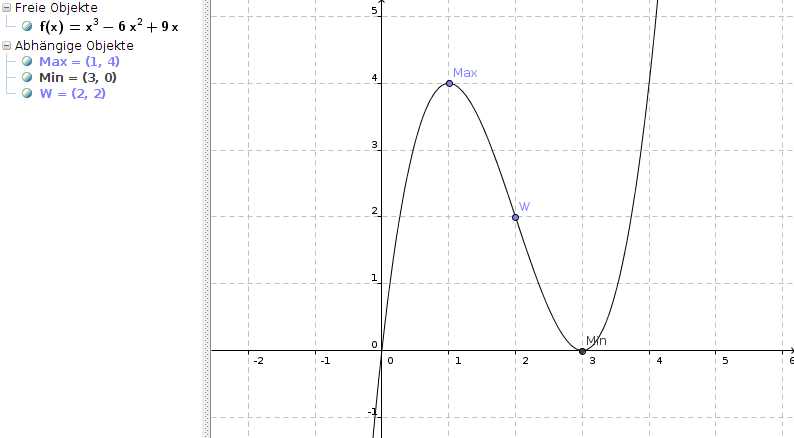
f(x) = x3 - 6x2 + 9x
Ges.:Symmetrie, Nullstellen, Extrema, Wendepunkte.
Symmetrie: Keine Symmetrie, da sowohl grad- als auch ungradzahlige Exponenten von x - richtig!
Nullstellen:
f(x) = x3 - 6x2 + 9x = x * (x2 - 6x + 9)
Erste Nullstelle also x0 = 0
x2 - 6x + 9 = 0 | pq-Formel
x1,2 = 3 ± √(9-9) = 3 ±√0
Zweite Nullstelle (doppelte Nullstelle) also x1 = 3
Extrema:
1. Ableitung = 0, zweite Ableitung ≠ 0
f'(x) = 3x2 - 12x + 9 = 0
x2 - 4x + 3 = 0 | pq-Formel
x1,2 = 2 ± √(4-1)
x1 = 3
x2 = 1
f''(x) = 6x - 12
f''(3) = 18 - 12 = 6 > 0, also Minimum an (3|f(3)) = (3|0)
f''(1) = 6 - 12 = -6 < 0, also Maximum an (1|f(1)) = (1|4)
Wendepunkt:
f''(x) = 0, f'''(x) ≠ 0
6x - 12 = 0 | x = 2
f'''(x) = 6 | f'''(2) = 6 ≠ 0, also Wendepunkt an (2|f(2)) = (2|2)
Besten Gruß