Kettenregel: vereinfachen und ableiten

Question

Aufgabe:

Leiten Sie ab und vereinfachen Sie das Ergebnis

a) f(x) = (x + 2)^4

b) f(x) = (8x + 2)^3

c) f(x) = (1/2 - 5x)^3

d) f(x) = 1/4(x^2 - 5)^2

Problem/Ansatz:

Wir behandeln in Mathe gerade die Kettenregel im Bereich Analysis.

Ich habe die Aufgaben schon probiert zu lösen, bin mir aber allerdings total unsicher, ob das richtig ist. Ich würde freuen, wenn jemand da mal drüber schauen könnte und mir falls es falsch ist weiterhelfen kann.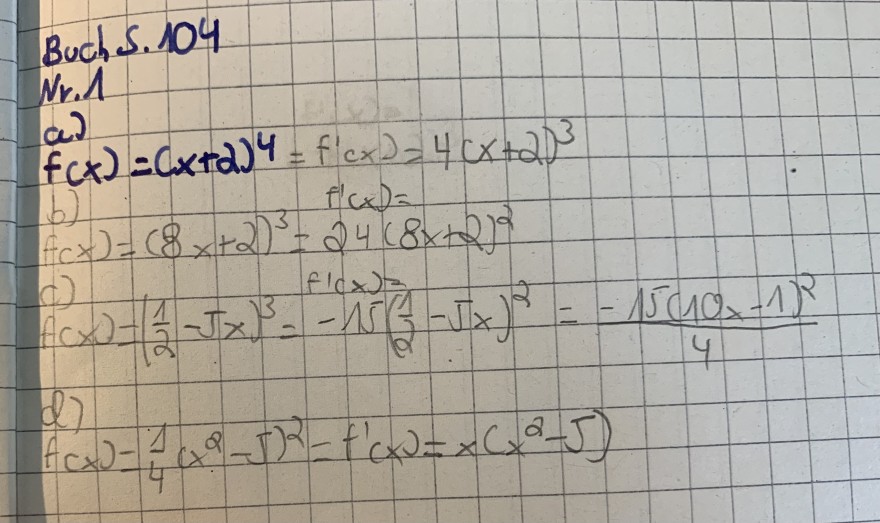

Text erkannt:

Buch S. 104
Nr. 1
\( f(x)=(x+2)^{4}=f^{\prime}(x)=4(x+2)^{3} \)
\( f(x)=(8 x+2)^{3}=24(8 x+2)^{2} \) \( f(x)=(x)= \)
\( f(x)=\left(\frac{1}{2}-\sqrt{x}\right)^{3}=-15\left(\frac{1}{2}-\sqrt{x}\right)^{2}=\frac{-15(10 x-1)^{2}}{4} \)

Answer 1

Aloha :)

Die innere Funktion habe ich jeweils in pink dargestellt und die Ableitung dieser inneren Funktion in grün:

$$f(x)=(\pink{x+2})^4\implies f'(x)=4(\pink{x+2})^3\cdot\green1=4(x+2)^3$$$$f(x)=(\pink{8x+2})^3\implies f'(x)=3(\pink{8x+2})^2\cdot\green8=24(8x+2)^2$$$$f(x)=\left(\pink{\frac12-5x}\right)^3\implies f'(x)=3\left(\pink{\frac12-5x}\right)^2\cdot\green{(-5)}=-\frac{15}{4}(10x-1)^2$$$$f(x)=\frac14(\pink{x^2-5})^2\implies f'(x)=\frac12(\pink{x^2-5})\cdot\green{2x}=x(x^2-5)$$

Alle deine Ergebnisse sind richtig.\(\quad\checkmark\)

Comments

Vielen lieben Dank für Ihre Hilfe!

Answer 2

gelöschttttttttttttttttttttttttttttttttt