Aufgabe:
Wie muss das maximale Gewinn verändert werden, damit ein faires Spiel entsteht?
Problem/Ansatz
hier sind die Wahrscheinlichkeiten, ist das höchste Gewinn Maximum also 3? X=3
wenn ja sieht mein Lösungsweg wie folgt aus:
0•1/30+1•3/10+2•1/2+x•1/6
danach zusammenrechnen
3/10 + 1 + 1/6 und dann gleich null setzten oder?
13/16+1/6x= 0 : 13/10
1,6x = -13/10 : 1,6
Als Ergebnis habe ich -7,8 raus
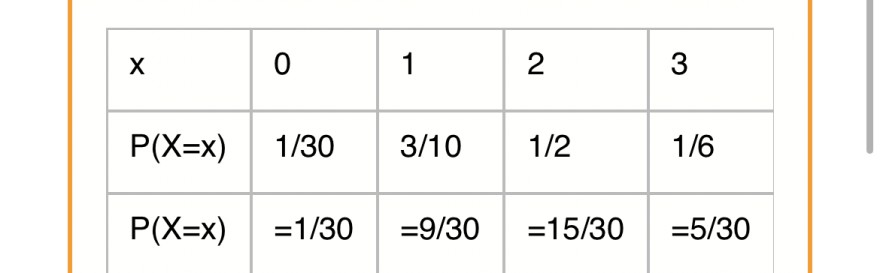
Text erkannt:
\begin{tabular}{|l|l|l|l|l|}
\hline\( x \) & 0 & 1 & 2 & 3 \\
\hline\( P(X=x) \) & \( 1 / 30 \) & \( 3 / 10 \) & \( 1 / 2 \) & \( 1 / 6 \) \\
\hline\( P(X=x) \) & \( =1 / 30 \) & \( =9 / 30 \) & \( =15 / 30 \) & \( =5 / 30 \) \\
\hline
\end{tabular}