Aufgabe:
Urne A enthält zwei weiße und zwei schwarze Kugeln. Urne B enthält drei weiße und zwei schwarze Kugeln.
Eine Kugel wird von Urne A nach Urne B transferiert. Danach wird eine Kugel aus Urne B gezogen.
(a) Wie hoch ist die Wahrscheinlichkeit, dass die gezogene Kugel weiß ist?
(b) Gegeben die gezogene Kugel ist weiß. Wie hoch ist die Wahrscheinlichkeit, dass die transferierte
Kugel auch weiß ist?
Problem/Ansatz:
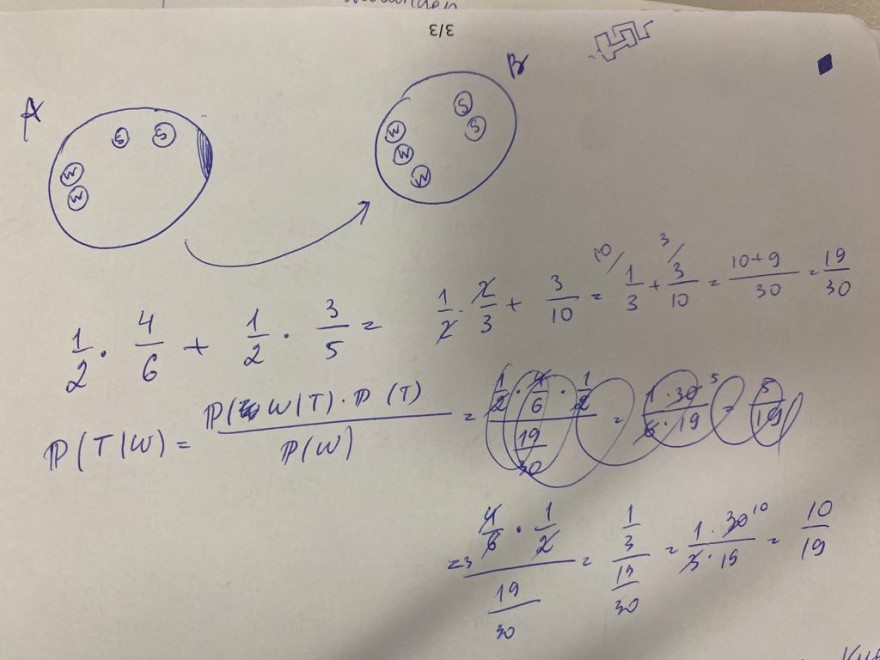
Text erkannt:
\( \begin{array}{l}\frac{1}{2} \cdot \frac{4}{6}+\frac{1}{2} \cdot \frac{3}{5}=\frac{1}{2} \cdot \frac{x}{3}+\frac{3}{10}=\frac{1}{3}+\frac{3}{10}=\frac{10+9}{30}=\frac{19}{30} \\ \mathbb{P}(T \mid \omega)=\frac{\mathbb{P}(W|T) \cdot \mathbb{P}(T)}{\mathbb{P}(\omega)}=\frac{\frac{4}{6} \cdot \frac{1}{2}}{\frac{19}{30}}=\frac{1 \cdot 30}{3 \cdot 19}=\frac{10}{19}\end{array} \)
hab solche Ergebnisse bekommen, aber bin nicht sicher :´)
LG