Wo liegen denn konkret die Probleme
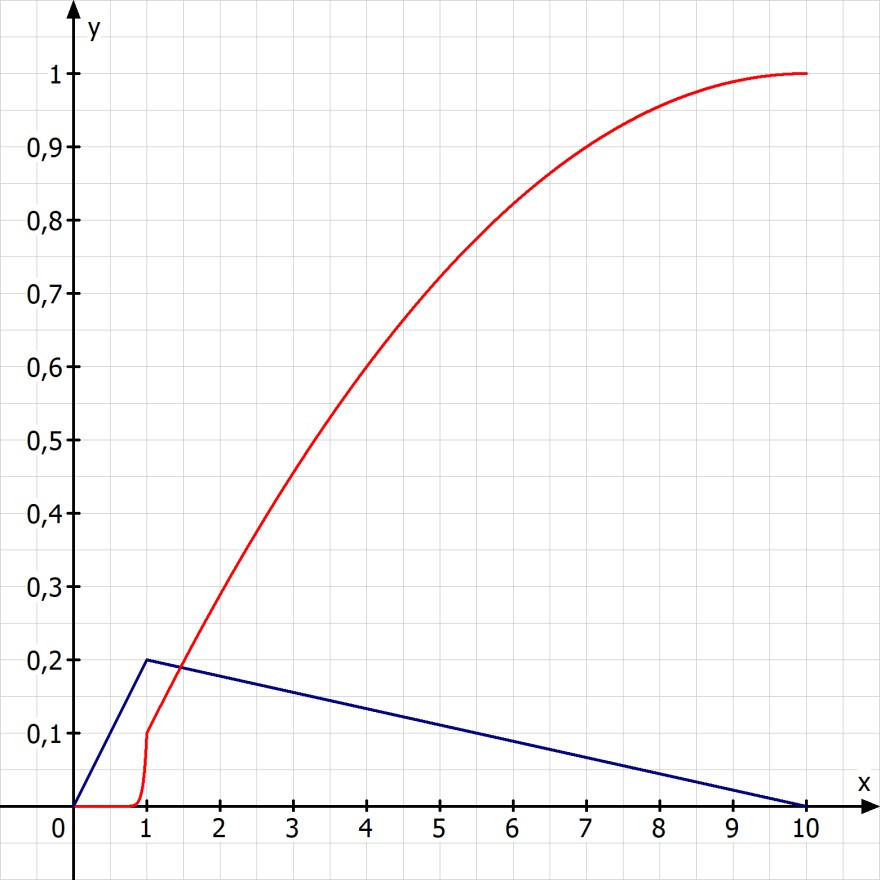
Zeichnen Sie sie diese Dichtefunktion. Kannst du die Dichtefunktion nicht als zwei lineare Funktionen zeichnen. Für eine lineare Funktion brauchst du nur 2 Punkte bestimmen und diese mit einer Gerade im Definitionsbereich verbinden.
Weißt du das die Ableitung der Verteilungsfunktion die Dichtefunktion ist?
Wie bekommt man dann aus der Dichtefunktion die Verteilungsfunktion?
Aber eigentlich wär das schon mehr als du machen sollst. Du sollst ja nur die Verteilungsfunktion an drei Stellen bestimmen und das bedeutet nur einfaches Kästchen zählen.
Dichte- und Verteilungsfunktion