Wie groß ist die Wahrscheinlichkeit, dass genau 3 von diesen 15 Bauteilen defekt sind?

Question

Aufgabe:

In einem Betrieb werden Bauteile produziert. Man weiß aus Erfahrung, dass 8% der Bauteile defekt sind. Nun werden 15 Bauteile zufällig ausgewählt und überprüft.

1. Wie groß ist die Wahrscheinlichkeit, dass genau 3 von diesen 15 Bauteilen defekt sind?

2. Wie groß ist die Wahrscheinlichkeit, dass darunter höchstens ein defektes Bauteil dabei ist.

3. (Extra Aufgabe)

Ein anderer Schüler hat einen alternativen Rechensatz für Aufgabe 1. gefunden:

Interpretieren Sie diesen Ansatz. Hat das Auswirkungen auf das Rechenergebnis?

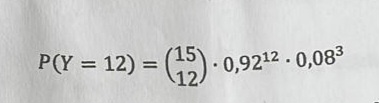
Text erkannt:

\( P(Y=12)=\left(\begin{array}{l}15 \\ 12\end{array}\right) \cdot 0,92^{12} \cdot 0,08^{3} \)

Hey Leute, Ich sitze schon lange an dieser Aufgabe, aber bekomme die ganze Zeit das falsche Ergebnis raus. Wäre dankbar für jede Antwort/Hilfe.

Schönes Wochenende euch :)

Answer 1

1. (15über3)*0,08^3*0,92^12

2. P(X<=1) = P(X=0) +P(X=1) = 0,92^15 + 15*0,08*0,92^14

3. (15über3) = (15über12)

https://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/binomialkoeffizienten

Regel 3

Answer 2

1. Wie groß ist die Wahrscheinlichkeit, dass genau 3 von diesen 15 Bauteilen defekt sind?

P(X = 3) = (15 über 3)·0.08^3·0.92^12 = 0.08565

2. Wie groß ist die Wahrscheinlichkeit, dass darunter höchstens ein defektes Bauteil dabei ist.

P(X ≤ 1) = 0.08^0·0.92^15 + 15·0.08^1·0.92^14 = 0.6597

3. Ein anderer Schüler hat einen alternativen Rechensatz für Aufgabe 1. gefunden: Interpretieren Sie diesen Ansatz. Hat das Auswirkungen auf das Rechenergebnis?

Wenn genau 3 von 15 Bauteilen defekt sind, dann sind auch genau 12 von 15 Bauteilen heil. Der Schüler berechnet also einfach die Wahrscheinlichkeit, dass 12 heil sind und erhält exakt dasselbe Ergebnis.