Hey, seht ihr vielleicht, welche Regel hier angewendet wurde, um die Kovarianz mittels des Erwartungswerts auszudrücken? Ist die Umformung vielleicht eine Abwandlung dieser Regel: Cov(X,Y)=E[(X-E[X])(Y-E[Y])]?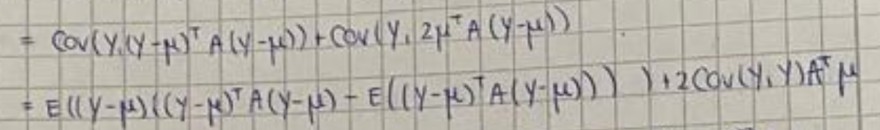
VG
Text erkannt:
\( \begin{array}{l}=\operatorname{Cov}\left(y,(y-\mu)^{\top} A(y-\mu)\right)+\operatorname{cov}\left(y, 2 \mu^{\top} A(y-\mu)\right) \\ =E\left((y-\mu)\left((y-\mu)^{\top} A(y-\mu)-E\left((y-\mu)^{\top} A(y-\mu)\right)\right)\right)+2 \operatorname{cov}(y, y) A^{\top} \mu\end{array} \)