Der Mediant zweier gegebener Brüche ist ein Bruch in dessen Zähler die Summe der gegebenen Zähler und in dessen Nenner die Summe der gegebenen Nenner steht. Der Mediant zweier Brüche unterschiedlicher Größe ist immer größer als der kleinere und kleiner als der größere. Medianten eignen sich auch, um irrationale Zahlen rational einzuschachteln. Das soll am Beispiel der Einschachtelung von √2 vorgeführt werden. Die erste Einschachtelung soll mit 1/1<√2<3/2 gegeben sein. Der Mediant der einschachtelnden Brüche ist dann 4/3, also kleiner als √2. Damit ergibt sich die verbesserte Einschachtelung 4/3<√2<3/2.
Auch hier ist der Mediant 7/5 kleiner als √2. Damit wird die Einschachtelung noch weiter verbessert zu 7/5<√2<3/2. Der nächste Mediant 10/7 ist indessen größer als √2 und auch der daraus gefolgerte Mediant der anschließenden Einschachtelung ist größer als √2. Um nicht bei jeder neuen Mediantenbildung herausfinden zu müssen, ob eine zu kleine oder eine zu große Grenze der Einschachtelung gefunden wurde, merkt man sich, dass auf zwei zu kleine Schachtelgrenzen zwei zu große folgen und umgekehrt.
Es ergibt sich die folgende Darstellung der Einschachtelung, in der die farbigen Linien von zwei Brüchen zu ihrem Medianten führen:
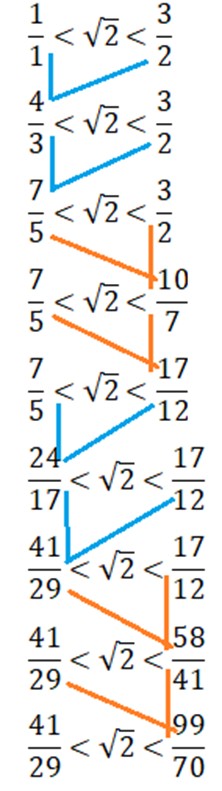
Man muss allerdings erkennen, dass der Fortschritt der Einschachtelung nicht groß ist, wie beim Heron-Verfahren.