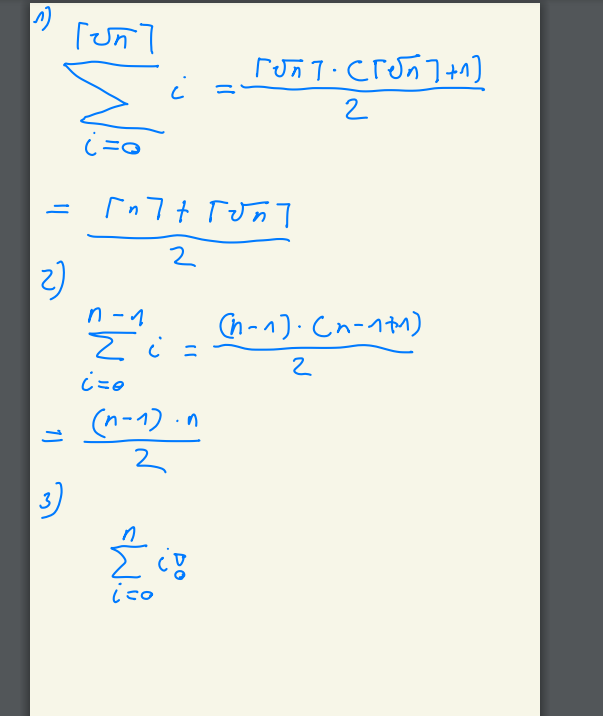
Text erkannt:
1)
\( \sum \limits_{i=0}^{\lceil\sqrt{n}\rceil} i=\frac{\lceil\sqrt{n} 7 \cdot([\sqrt{n}\rceil+1]}{2} \)
\( =\frac{\Gamma_{n} 7+\Gamma \sqrt{n} 7}{2} \)
2)
\( \begin{aligned} & \sum \limits_{i=0}^{n-1} i=\frac{(n-1) \cdot(n-1+1)}{2} \\ = & \frac{(n-1) \cdot n}{2} \end{aligned} \)
ich will alle drei Summen in die Gaußsche Summenformel bringen, kann mir jemand zu den ersten beiden Umformungen Feedback geben bzw. Verbesserungsvorschläge, bei der 3 ist mir leider nicht wirklich was eingefallen, da auch bitte Tipps.