Grafisches Differenzieren - Bestimmen der Ableitungsfunktion.

Question

Aufgabe:

Grafisches Differenzieren - Bestimmen der Ableitungsfunktion

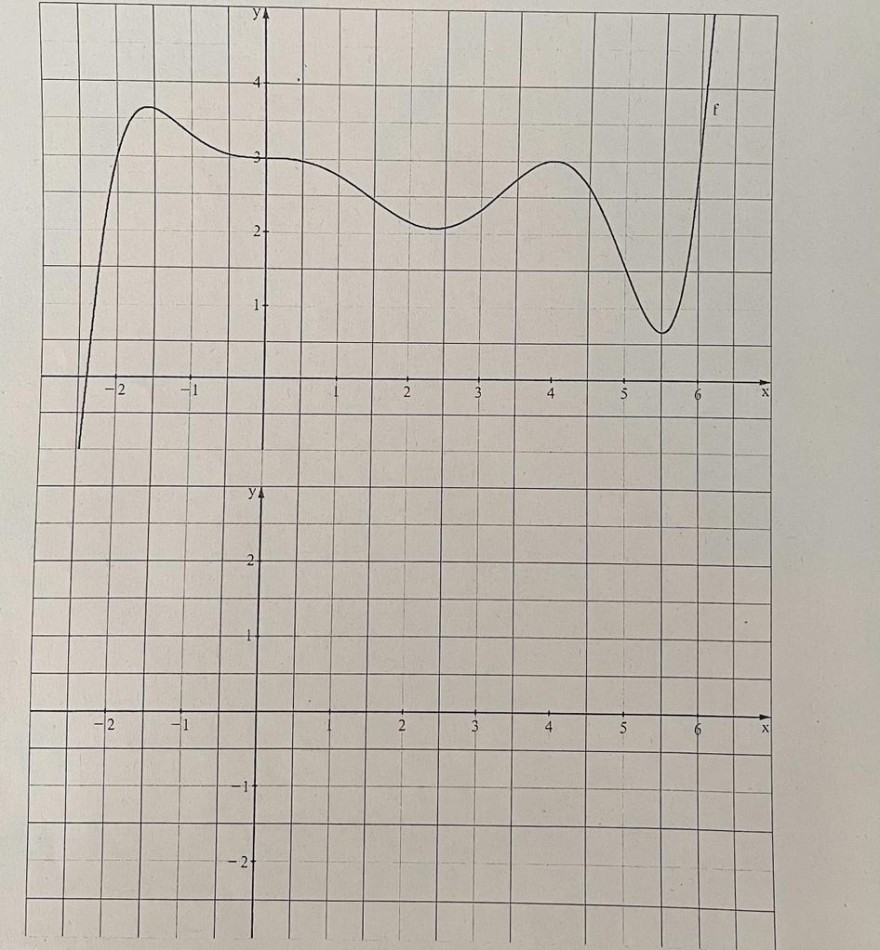
In der Abbildung ist der Graph einer Funktion \( f \) gegeben.

a) Bestimmen Sie die Steigungen der Tangenten in den Hochpunkten, Tiefpunkten und Sattelpunkten des Funktionsgraphen; sowie in weiteren selbst gewählten Punkten.

Tragen Sie die Werte in das untere Koordinatensystem ein und verbinden Sie die Punkte zum Graphen der Ableitungsfunktion.

Problem/Ansatz:

hab Problem dabei wie kann ich’s am besten mache?

Answer 1

Der Graph und die Ableitung sehen in etwa wie folgt aus:

Answer 2

In den genannten Punkten ist die Steigung m= 0.

Bedingung ist in allen Fällen. f '(x)= 0

Beim Sattelpunkt gilt zudem: f ''(x) = 0 , er hat die Koordinaten S(0/3)

Comments

Danke, könntest du mir noch den Funktionsterm der Funktion sagen?

Answer 3

Hallo

1. die 5 waagerechten Stellen  also f'=0 sind ja wohl leicht. An einigen Stellen die Tangente anlegen und die Steigungen bestimmen und dann die Zahl als y Wert von f' eintragen auch.  Also was fehlt dir?

die Ableitung fängt bei -2,4 mit einem hohen Wert an fällt dann bis ca x=-1,7 auf 0 ab da negativ bis sie bei 0 wieder 0 wird  usw.

lul

Comments

Danke, aber ich verstehe nicht genau, wie ich das grafische Differenzieren mache

---

Hallo

genau das habe ich doch erklärt? aus der gegebenen Graphik die Steigungen ablesen und die Werte bei den entsprechenden x Stellen einzeichnen. dann sinnvoll die Punkte verbinden.ergibt den Graphen von f'

lul

---

Danke, könntest du mir noch den Funktionsterm der Funktion sagen?

---

Hallo

nein, das kann man nicht so einfach, so eine Funktion kann man zeichnen ohne eine funktiojnsterm zu kennen, das ist ja auch nicht gefragt.  Wenn es ein Polynom ist, dann mindestens 6ten Grades.

lul