Funktion vervollständigen und m Wert herausfinden.

Question

Aufgabe:

Der Graph einer Funktion g mit g(x) = mx + 2,5 (m ∈IR) schneidet die
Koordinatenachsen in den Punkten N und S. Die Punkte N und S bilden mit dem
Koordinatenursprung die Eckpunkte eines Dreiecks.
Gib für m eine Zahl an, damit dieses Dreieck gleichschenklig ist.

Problem/Ansatz:

Answer 1

Achsenabschnittsform der Geraden:

$\frac{x}{a}+\frac{y}{b}=1$

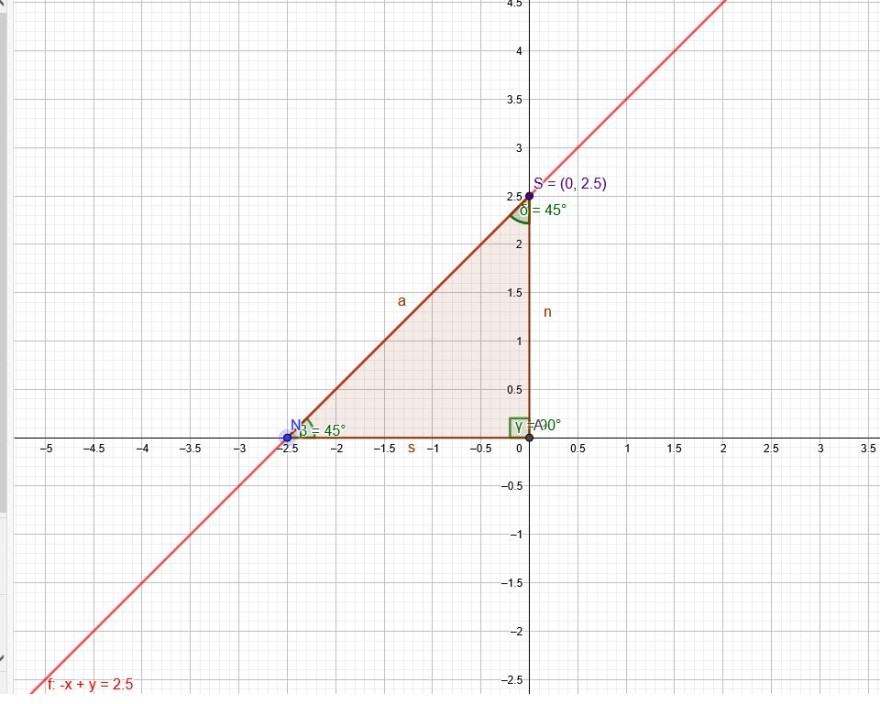
$y=m*x+2,5$

Umwandeln in die Achsenabschnittsform der Geraden:

$-m*x+y=2,5 |:2,5$

$-\frac{m}{2,5}*x+\frac{y}{2,5}=1 |$

$-\frac{x}{\frac{2,5}{m}}+\frac{y}{2,5}=1$

Damit ein gleichschenkliges Dreieck entsteht, muss$\frac{2,5}{m} =2,5$sein.

Das ist bei $m=1$ der Fall.

$y=x+2,5$

Answer 2

g(-2,5) = 0

m*(-2,5)+2,5= 0

= 1

g(x) = x+2,5

Die x und y-Koordinate haben denselben Betrag.

oder:

g(2,5) = 0

g(x) = -x+2,5