Aufgabe:
Problem/Ansatz:
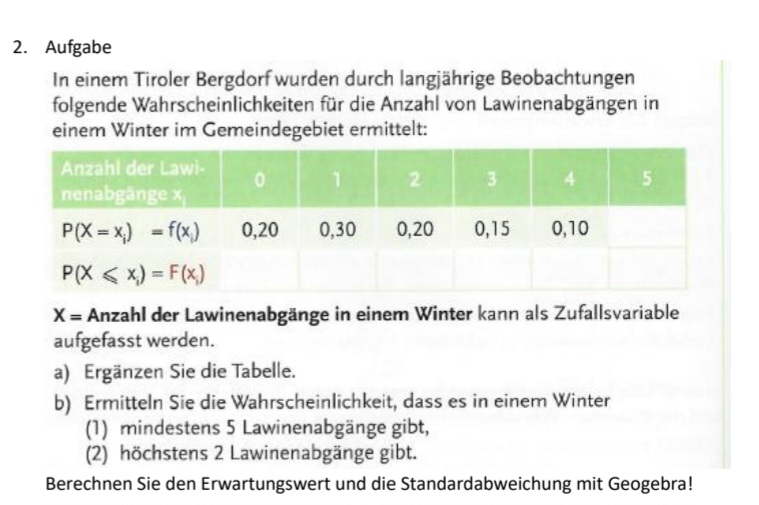
Text erkannt:
2. Aufgabe
In einem Tiroler Bergdorf wurden durch langjährige Beobachtungen folgende Wahrscheinlichkeiten für die Anzahl von Lawinenabgängen in einem Winter im Gemeindegebiet ermittelt:
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline \( \begin{array}{l}\text { Anzahl der Lawi- } \\ \text { nenabgange } x\end{array} \) & 0 & 1 & 2 & 3 & 4 & 5 \\
\hline\( P\left(X=x_{i}\right)=f\left(x_{i}\right) \) & 0,20 & 0,30 & 0,20 & 0,15 & 0,10 & \\
\hline\( P\left(X \leqslant x_{1}\right)=F\left(x_{1}\right) \) & & & & & & \\
\hline
\end{tabular}
\( X= \) Anzahl der Lawinenabgänge in einem Winter kann als Zufallsvariable aufgefasst werden.
a) Ergänzen Sie die Tabelle.
b) Ermitteln Sie die Wahrscheinlichkeit, dass es in einem Winter
(1) mindestens 5 Lawinenabgänge gibt,
(2) höchstens 2 Lawinenabgänge gibt.
Berechnen Sie den Erwartungswert und die Standardabweichung mit Geogebra!