Aufgabe:
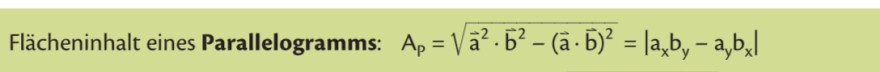
Text erkannt:
Flächeninhalt eines Parallelogramms: \( \quad A_{p}=\sqrt{\vec{a}^{2} \cdot \vec{b}^{2}-(\vec{a} \cdot \vec{b})^{2}}=\left|a_{x} b_{y}-a_{y} b_{x}\right| \)

Text erkannt:
Ermittle die fehlenden Koordinaten sowie den Flächeninhalt des angegebenen Parallelogramms mithilfe der Vektorrechnung.
a) A(10|5), B(2|3), C \( \left(x_{C} \mid y_{C}\right), D(13 \mid 5) \)
Hey Leute, ich habe die fehlenden Koordinaten berechnet C(5|3)
Ich verstehe jetzt diesen Formel nicht bzw. was ich wo genau einsetzen muss, um die Flächeninhalt zu berechnen.
Könnt ihr mir bei einsetzen die Werte in der Formel helfen? Danke!