Aufgabe:
Taylorpolynom
Könnt ihr bitte rüberschauen ob das ergebnis so richtig ist. 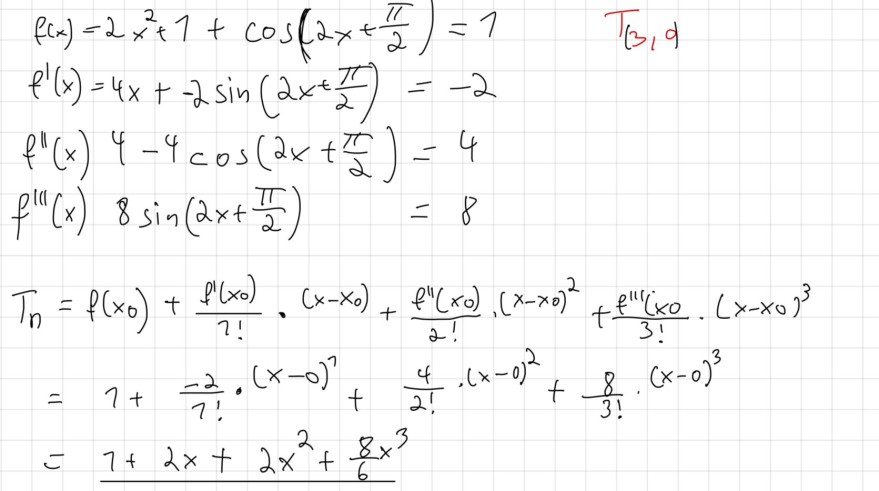
Text erkannt:
\( \begin{array}{l}f(x)=2 x^{2}+1+\cos \left(2 x+\frac{\pi}{2}\right)=1 \quad T_{(3,9} \\ f^{\prime}(x)=4 x+-2 \sin \left(2 x+\frac{\pi}{2}\right)=-2 \\ f^{\prime \prime}(x) 4-4 \cos \left(2 x+\frac{\pi}{2}\right)=4 \\ f^{\prime \prime \prime}(x) 8 \sin \left(2 x+\frac{\pi}{2}\right)=8 \\ T_{n}=f\left(x_{0}\right)+\frac{f^{\prime}\left(x_{0}\right)}{1 !} \cdot\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !} \cdot\left(x-x_{0}\right)^{2}+\frac{f^{\prime \prime \prime}\left(x_{0}\right.}{3 !} \cdot\left(x-x_{0}\right)^{3} \\ =1+\frac{-2}{1 !} \cdot(x-0)^{1}+\frac{4}{2 !} \cdot(x-0)^{2}+\frac{8}{3 !} \cdot(x-0)^{3} \\ =1+2 x+2 x^{2}+\frac{8}{6} x^{3}\end{array} \)
Sehe gerade am ende das vorzeichen von der 2 ist falsch es sollte -2 sein
Problem/Ansatz: