Aufgabe:
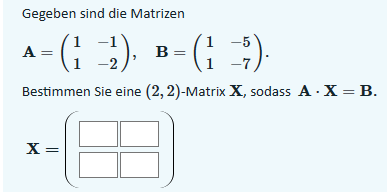
Text erkannt:
Gegeben sind die Matrizen
\( \mathbf{A}=\left(\begin{array}{ll} 1 & -1 \\ 1 & -2 \end{array}\right), \quad \mathbf{B}=\left(\begin{array}{ll} 1 & -5 \\ 1 & -7 \end{array}\right) \)
Bestimmen Sie eine (2,2)-Matrix \( \mathbf{X} \), sodass \( \mathbf{A} \cdot \mathbf{X}=\mathbf{B} \).
Problem/Ansatz:
Ich habe es mit folgendem Ansatz probiert: A-1*B =X. Jedoch ist Lösung falsch, weil ich evtl. falsch gerechnet habe, jedoch finde ich keinen Fehler.
Könnt ihr mir den Lösungsweg zeigen?