Aufgabe:
Berechnen des Minimalpolynoms
Problem/Ansatz:
Gegeben sei der Endomorphismus \( f: \mathbb{R}^{3 \times 1} \rightarrow \mathbb{R}^{3 \times 1} \) mit Darstellungsmatrix
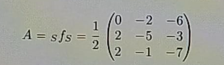
bzgl. des Standadkoordinatensystems \( S=\left(e_{1}, e_{2}, e_{3}\right) \). Es gilt (das müssen Sie nicht nachrechnen)
Text erkannt:
\( A=s f_{S}=\frac{1}{2}\left(\begin{array}{lll}0 & -2 & -6 \\ 2 & -5 & -3 \\ 2 & -1 & -7\end{array}\right) \)

Text erkannt:
\( \chi_{f}=-(x+2)^{3} \quad \) und \( \quad\left(\begin{array}{l}3 \\ 0 \\ 2\end{array}\right) \in \operatorname{Eig}(f,-2) \)
(a) Berechnen Sie das Minimalpolynom \( \mu_{f} \) von \( f \).
(b) Ist \( f \) diagonalisierbar? Geben Sie eine Jordan-Normalform \( J \) von \( f \) an.
(c) Berechnen Sie ein Koordinatensystem \( B \) von \( \mathbb{R}^{3 \times 1} \) mit \( { }_{B} f_{B}=J \).
Text erkannt:
Aufgabe 6.2: (Abgabeaufgabe) Klausuraufgabe im SoSe 2017 (gab 24,Punkte):
Gegeben sei der Endomorphismus \( f: \mathbb{R}^{3 \times 1} \rightarrow \mathbb{R}^{3 \times 1} \) mit Darstellungsmatrix
\( A=s f_{S}=\frac{1}{2}\left(\begin{array}{lll} 0 & -2 & -6 \\ 2 & -5 & -3 \\ 2 & -1 & -7 \end{array}\right) \)
bzgl. des Standadkoordinatensystems \( S=\left(e_{1}, e_{2}, e_{3}\right) \). Es gilt (das müssen Sie nicht nachrechnen)
\( \chi_{f}=-(x+2)^{3} \quad \text { und } \quad\left(\begin{array}{l} 3 \\ 0 \\ 2 \end{array}\right) \in \operatorname{Eig}(f,-2) \text {. } \)
(a) Berechnen Sie das Minimalpolynom \( \mu_{f} \) von \( f \).
(b) Ist \( f \) diagonalisierbar? Geben Sie eine Jordan-Normalform \( J \) von \( f \) an.
(c) Berechnen Sie ein Koordinatensystem \( B \) von \( \mathbb{R}^{3 \times 1} \) mit \( { }_{B} f_{B}=J \).
Aufgabe von der Uni, komme hier nicht ganz weiter. Sowohl a, b, als auch c.