Hochpunkt von f_{0} bei der Funktion f_{t}(x)= e^{-x} · (x-t)

Question

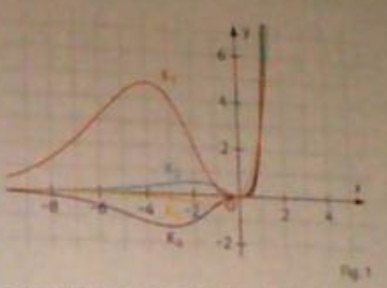
Die Abbildung zeigt fünf Graphen der Funktionenschar mit \( f_{t}(x)=e^{-x} · (x-t) \cdot \)

a) Ordnen Sie die Funktionen \( f_{0} \) und \( f_{2} \) ihren Graphen zu. Begründen Sie.

b) Bestimmen Sie den Hochpunkt der Graphen von \( f_{0} \) und \( f_{2} \) und seigen Sie, dass die Hochpunkte auf dem Graphen von \( \mathrm{g} \) mit \( g(x) = e^{-x} \) liegen.

c) Zeigen Sie, dass sich \( \mathrm{f}_{0} \) und \( f_{2} \) nicht schneiden.

Answer 1

ft(x) = e^{-x}·(x - t)

ft'(x) = - e^{-x}·(x - t - 1)

f''(x) = e^{-x}·(x - t - 2)


Extrempunkte ft'(x) = 0

x - t - 1 = 0

x = t + 1

f(t + 1) = e^{-x}·(x - t) = e^{-(t + 1)}·((t + 1) - t) = e^{- t - 1} = 1/e^{t + 1}

f''(t + 1) = e^{-x}·(x - t - 2) = e^{-(t + 1)}·((t + 1) - t - 2) = - e^{-t - 1} < 0 → Hochpunkt


Ortskurve der Extrempunkte

x - t - 1 = 0

t = x - 1

Jetzt für t das x - 1 in die Funktion einsetzen

f(x) = e^{-x}·(x - (x - 1)) = e^{-x}


Aller klar ?