Aufgabe:
Text erkannt:
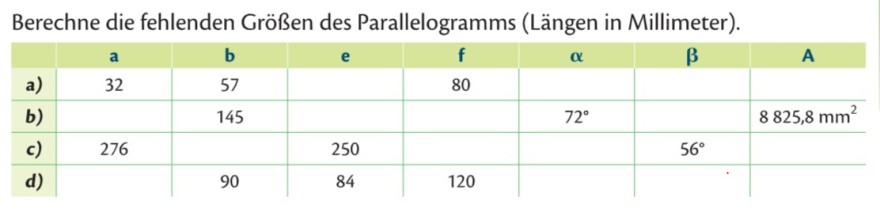
Berechne die fehlenden Größen des Parallelogramms (Längen in Millimeter).
\begin{tabular}{|l|c|c|c|c|c|c|c|c|}
\hline & \( \mathbf{a} \) & \( \mathbf{b} \) & \( \mathbf{e} \) & \( \mathbf{f} \) & \( \boldsymbol{\alpha} \) & \( \boldsymbol{\beta} \) & \( \mathbf{A} \) \\
\hline a) & 32 & 57 & & 80 & & & \\
\hline b) & & 145 & & & \( 72^{\circ} \) & & \( 8825,8 \mathrm{~mm}^{2} \) \\
\hline c) & 276 & & 250 & & & \( 56^{\circ} \) & \\
\hline d) & & 90 & 84 & 120 & & & \\
\hline
\end{tabular}
Problem/Ansatz:
Hey Leute, gibt es bei Parallelogramms auch wie allgemeine Dreieck so Formen wie man die fehlenden Seiten berechnen kann?
Wenn ja wie lauten die Formeln und wenn nicht wie soll ich die Aufgabe lösen?