Aufgabe:
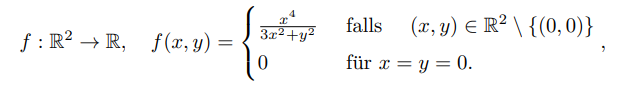
Text erkannt:
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll}\frac{x^{4}}{3 x^{2}+y^{2}} & \text { falls } \quad(x, y) \in \mathbb{R}^{2} \backslash\{(0,0)\} \\ 0 & \text { für } x=y=0\end{array}\right. \)
Problem/Ansatz:
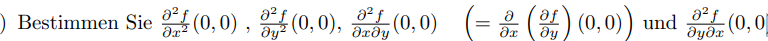
Text erkannt:
Bestimmen Sie \( \frac{\partial^{2} f}{\partial x^{2}}(0,0), \frac{\partial^{2} f}{\partial y^{2}}(0,0), \frac{\partial^{2} f}{\partial x \partial y}(0,0) \quad\left(=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)(0,0)\right) \) und \( \frac{\partial^{2} f}{\partial y \partial x}(0,0 \)
Wie bestimmt man die 2. Ableitung, wenn unten x2 und y2 steht?