Hallo,
Nach den Eigenwerten müssen die Eigenvektoren(Hauptvektoren) berechnet werden,
weil 3 eine doppelte Lösung ist.

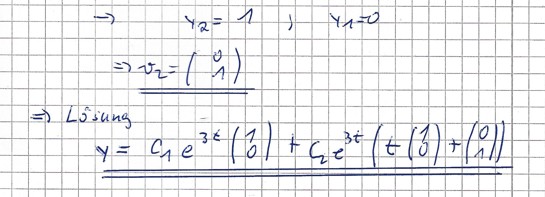
Die Lösung ist die homogene Lösung:
Ansatz part. Lösung:
y1= (a t^2 +bt +c) e^(6t)
y2= (A t^2 +Bt +C) e^(6t)
------>in die Aufgabe einsetzen, Koeffizientenvergleich

y=yh+yp
Gesamtlösung:
\( \begin{array}{c}y_{1}=\frac{t^{2} e^{6 t}}{3}-\frac{t e^{6 t}}{9}+C_{2} t e^{3 t}+C_{1} e^{3 t} \\ y_{2}=\frac{t e^{6 t}}{3}-\frac{e^{6 t}}{9}+C_{2} e^{3 t}\end{array} \)