Aufgabe:

Problem/Ansatz:
Ich bin auf folgendes gekommen:
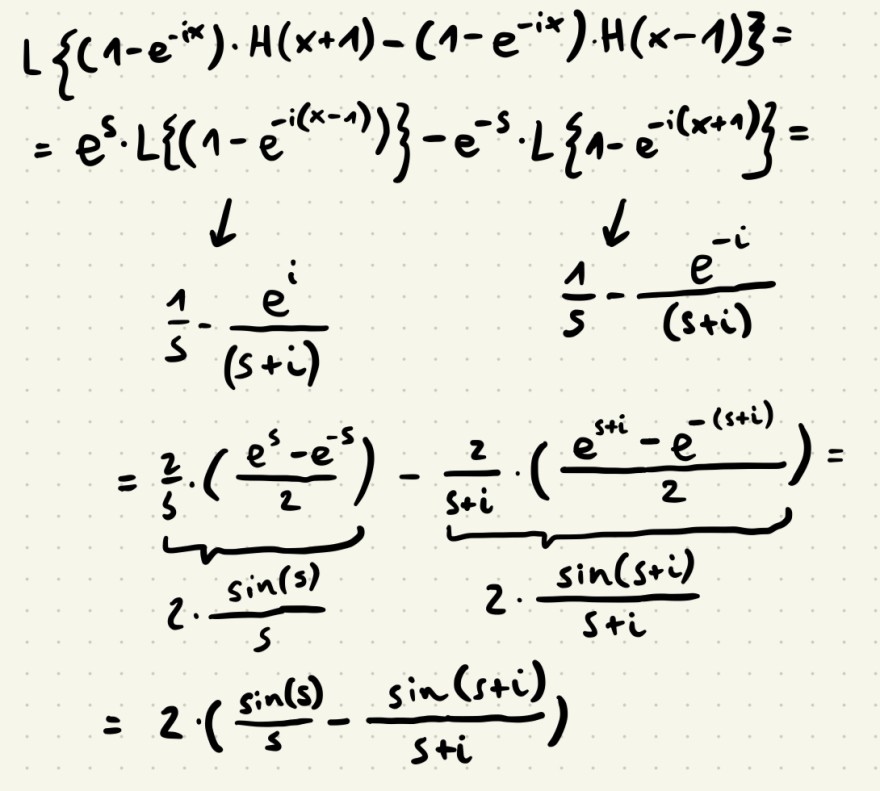
Text erkannt:
\( \begin{array}{l}L\left\{\left(1-e^{-i x}\right) \cdot H(x+1)-\left(1-e^{-i x}\right) \cdot H(x-1)\right\}= \\ =e^{s} \cdot L\left\{\left(1-e^{-i(x-1)}\right)\right\}-e^{-s} \cdot L\left\{1-e^{-i(x+1)}\right\}= \\ \frac{1}{s}-\frac{e^{i}}{(s+i)} \quad \frac{1}{s}-\frac{e^{-i}}{(s+i)} \\ =\underbrace{\frac{2}{s} \cdot\left(\frac{e^{s}-e^{-s}}{2}\right)}_{2 \cdot \frac{\sin (s)}{s}}-\underbrace{\frac{2}{s+i} \cdot\left(\frac{e^{s+i}-e^{-(s+i)}}{2}\right)}_{2 \cdot \frac{\sin (s+i)}{s+i}}= \\ =2 \cdot\left(\frac{\sin (s)}{s}-\frac{\sin (s+i)}{s+i}\right) \\\end{array} \)
Ist dies richtig und falls ja wie komme ich auf a) was richtig wäre?