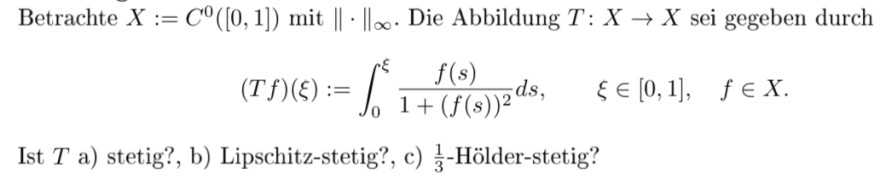
Text erkannt:
Betrachte \( X:=C^{0}([0,1]) \) mit \( \|\cdot\|_{\infty} \). Die Abbildung \( T: X \rightarrow X \) sei gegeben durch
\( (T f)(\xi):=\int \limits_{0}^{\xi} \frac{f(s)}{1+(f(s))^{2}} d s, \quad \xi \in[0,1], \quad f \in X . \)
Ist \( T \) a) stetig?, b) Lipschitz-stetig?, c) \( \frac{1}{3} \)-Hölder-stetig?
Könnte mir hier jemand helfen?