Bestimme die Wahrscheinlichkeit 3 der vier Asse zu ziehen

Question

Aufgabe:

Aus einem Pokerspiel mit insgesamt 52 Karten werden hintereinander zehn Karten

Die gezogene Karte wird wieder in den Kartenstapel zurückgesteckt. Wie groß ist die Wahrscheinlichkeit, dabei a) drei der vier Asse b) zwei der vier Könige c) alle vier Damen zu ziehen?

Problem/Ansatz:

Kann mir bitte jemand erklären wie man das rechnet?

Comments

...werden hintereinander zehn Karten

Da fehlt ein

---

Die Wahrscheinlichkeit, bei einer Ziehung die angegebene Kartenart zu ziehen, beträgt offenbar p=4/52. Dies ist bei allen drei Teilaufgaben jeweils gleich. Nennen wir p die Trefferwahrscheinlichkeit dieses Bernoulli-Versuchs. Die Anzahl n=10 der Ziehungen ist die Länge der entsprechenden Bernoulli-Kette. Sei X die Anzahl der Treffer bei den zehn Wiederholungen, dann ist X (n,p)-binomialverteilt. Gesucht ist dann zum Beispiel bei a) die Wahrscheinlichkeit P(X=3).

---

Gesucht ist dann zum Beispiel bei a) die Wahrscheinlichkeit P(X=3)

So einfach ist die Sache bei weitem nicht !

---

Oha, ich habe übersehen, dass die Karten ja verschieden sind und die Aufgabe somit ein Sammlerproblem beschreibt.

---

Also noch (4über3) bei a) ??

Rest analog?

---

@ggT22: Der Einspruch von Gast hj2166 hat mich bewegt, noch einmal ganz anders an die Aufgabe heranzugehen. Ich komme jetzt bei a) auf eine Wahrscheinlichkeit von etwa 0,010056. Ich bitte um kritische Kommentare!

---

Ich berichtige mich selbst: Ich komme auf etwa 0,015085.

---

Wie groß ist die Wahrscheinlichkeit, dabei a) drei der vier Asse b) zwei der vier Könige c) alle vier Damen zu ziehen?

Müssen bei a) die Asse unterschiedliche Symbole haben, oder gilt dreimal Herz-Ass als richtig?

Und dürfen bei den restlichen 7 gezogenen Karten Asse sein?

Entsprechend bei b und c.

---

@MontyPython: Ich bin davon ausgegangen, dass "dreimal Herz-Ass" zwar nicht verboten, aber ohne zwei weitere, voneinander verschiedene Asse nicht als Erfolg betrachtet wird.

---

Ich bitte um ... Kommentare!

Ich komme auf

p = \(4·3·2· \sum\limits_{n=3}^{10}{\frac{a_n}{52^n}} \) wobei a_n = \( \sum{b_1·b_2·b_3· ... b_{n-3}} \) mit den Bedingungen b₁ ≥ b₂ ≥ ... und b_k∈{48,49,50}
aber leider habe ich keine Ahnung von Wolframs Syntax.

---

Meine Rechnung zu a) (mit TI-Nspire CX Student Software):

$$\begin{pmatrix} \dfrac{48}{52}&0&0&0\\\\ \dfrac{4}{52}&\dfrac{49}{52}&0&0\\\\ 0&\dfrac{3}{52}&\dfrac{50}{52}&0\\\\ 0&0&\dfrac{2}{52}&\dfrac{52}{52} \end{pmatrix}^{10}\cdot \begin{pmatrix} 1\\0\\0\\0 \end{pmatrix}= \begin{pmatrix} 0.449137\\0.411392\\0.082924\\\red{0.010056}\end{pmatrix}$$ Das Ergebnis ist rot markiert.

---

Hier noch meine Überlegungen zur angegebenen Rechnung: Die Zustände 0, 1, 2 und 3 zählen das erstmalige Erscheinen von jeweils einem der vier Asse bei einer der zehn Ziehung. Dann ist 0 der Anfangs- und 3 der Endzustand. Daraus ergibt sich das folgende Zustandsübergangsdiagramm mit den zugehörigen Wahrscheinlichkeiten, auf dem die oben angegebene Übergangsmatrix beruht:

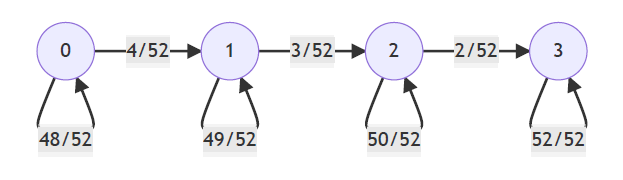
Im Zustand 3 befinden sich unter den zehn gezogenen Karten genau drei verschiedene Asse, die sich aber auch mehrmals zeigen durften.

---

Nun möchte ich natürlich wissen, ob meine Interpretation der Aufgabenstellung (Teil a) sinnvoll erscheint und ob mein Ansatz und meine Rechnung dazu zielführend bzw. richtig ist.

Mit dem Ansatz

Ich komme auf
p = \(4·3·2· \sum\limits_{n=3}^{10}{\frac{a_n}{52^n}} \) wobei a_n = \( \sum{b_1·b_2·b_3· ... b_{n-3}} \) mit den Bedingungen b_1 ≥ b_2 ≥ ... und b_k∈{48,49,50}

komme ich noch nicht zurecht; ich denke noch drüber nach.

---

Es ist im Wesentlichen derselbe wie deiner (allerdings ohne Markov und stattdessen mit Baumdiagramm ein gewaltiges Stück umständlicher).

Es wird die Wahrscheinichkeit berechnet, dass im n-ten Zug die drei Asse zum ersten Mal gezogen sind. Die ist z.B. für n=6 gegeben durch
p₆ = 4/52*3/52*2/52 * (50*50*50 + 49*50*50 + 49*49*50 + 49*49*49 + 48*50*50 + 48*49*50 + 48*49*49 +  48*48*50 + 48*48*49 + 48*48*48) / 52^3

Answer 1

a) n= 10, p= 4/52= 1/3, n= 3

(10über3)*(1/13)^3* (12/13)^7

b) (10über2)* (1/13)^2*(12/13)^8

c) (10über4)*(1/13)^4*(12/13)^6

Comments

Es weden zehn Karten gezogen, nicht zwölf und nicht neun.

---

a) n= 10, p= 4/52= 1/3, n= 3

Das klingt verstörend...